Vectores

Un vector x es un conjunto de n números reales

[x₁, x₂, ....x_n]

Geometricamente, representa un punto en el espacio Rⁿ, especificado por las n coordendas x₁, x₂, ....x_n.

En Física representamos un vector r en el espacio R³ respecto a un Sistema de Referencia Ortonormal formado por el origen O y tres vectores unitarios mutuamente perpendiculares. Las direcciones de estos vectores se denominan, ejes X, Y y Z, respectivamente.

$\vec{r} = 5 \hat{i} + 3 \hat{j} - 5 \hat{k}$

Los coeficientes de los vectores unitarios (las proyecciones del vector r sobre los ejes coordenados) son las coordendas (x, y, z) del punto P.

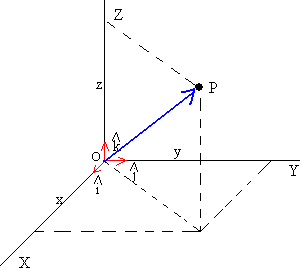
En MATLAB representamos un vector del siguiente modo

>> r=[5 3 -5]
r =     5     3    -5
>> r=[5,3,-5]
r =     5     3    -5

Para crear un vector fila se escribe sus elementos unos a continuación de los otros separados por espacios o comas y entre paréntesis cuadrados, tal como se muestra en el cuadro. Para crear un vector columna se escribe los elementos unos a continuación de los otros separados por puntos y comas o bien, en forma columna tal como se indica en el cuadro.

>> r=[5; 3; -5];
>> r=[5
3 
-5]
r =
     5
     3
    -5

Podemos convertir un vector fila en columna mediante el operador transpuesto '

>> r=[1,2,3]'
r =  1
     2
     3

Un vector con un espaciado constante Δx entre el primer término, x_i y el último término, x_f., se crea del siguiente modo:

vector=xi:Δx:xf

>> x=3:2:15
x = 3 5 7 9 12 15
>> y=2:-0.2:1  
y = 2.0000 1.8000 1.6000 1.4000 1.2000 1.0000
>> z=-5:3 % el espaciado por defecto es 1
y = -5 -4 -3 -2 -1 0 1 2 3

Creamos el vector

>> x=[0,0.38,0.71,0.92,1.00,0.92,0.71,0.38,0];

En la ventana Workspace vemos la variable x debajo de Name y los valores que guarda, debajo Value. Haciendo doble-clic sobre el nombre de la variable se abre un editor en forma de hoja de cálculo que nos permite modificar los valores de los elementos de dicho vector x

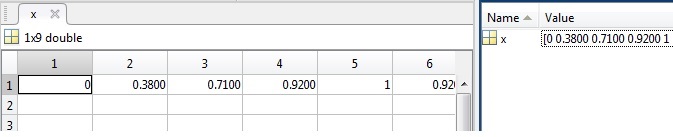
La función zeros(1,n) nos crea un vector fila formado por n ceros. La función zeros(n,1) nos crea un vector columna formado por n ceros. La función onesnos crea vectores formado por unos

>> zeros(1,5)
ans =     0     0     0     0     0
>> zeros(3,1)
ans =
     0
     0
     0
>> ones(1,4)
ans =     1     1     1     1

Acceso a los elementos de un vector

Cuando se crea un vector, por ejemplo x=[3,6,9,12,15,18]; la tabla muestra los indices del x y los valores que guardan los elementos del vector.

Indice	1	2	3	4	5	6
Valor	3	6	9	12	15	18

En general, un vector fila tiene la forma [r₁, r₂, r₃,....r_n]. Para acceder a un elemento i del vector r, r_i se escribe r(i). Para acceder la primer elemento se escribe r(1). Para acceder al último se escribe r(end). La función length devuelve el número de elementos del vector

>> r=[5 3 -5];
>> r(1)
ans =5
>> r(end)
ans =-5
>> length(r)
ans = 3

Con el operador : podemos acceder a más de un elemento del vector. Cuando escribimos v(m:n) se accede a los elementos del vector v desde las posiciones m hasta n. Es la forma de extraer un vector de otro vector. Por ejemplo, creamos un vector u con los elementos comprendidos entre las posiciones 3 y 7 ambas incluidas, de un vector v que tiene 10 elementos

>> v=[4 10 -3 7 -1 0 8 13 -7 0];
>> u=v(3:7)
u =    -3     7    -1     0     8

Creamos un vector u con los elementos de índice par del vector v.

>> v=[4 10 -3 7 -1 0 8 13 -7 0];
>> u=v(2:2:end)
u =    10     7     0    13     0

Podemos también crear un vector u a partir de otro vector de subíndices. Por ejemplo, crear un vector u tomando el elemento quinto, primero, cuarto y octavo elemento del vector v, en este orden.

>> v=[4 10 -3 7 -1 0 8 13 -7 0];
>> u=v([5 1 4 8])
u =    -1     4     7    13

Se pueden añadir elementos a un vector de la siguiente forma

>> v=1:4
v =     1     2     3     4
>> v(5:10)=7:3:22
v =     1     2     3     4     7    10    13    16    19    22
>> v(12)=-1
v =     1     2     3     4     7    10    13    16    19    22    0    -1

Si se sobrapasa la dimensión del vector que era 10, se le añade el elemento de índice 12, al elemento de índice 11 se le asigna automáticamente cero.

Creamos un vector a partir de otros dos vectores, insertamos un escalar (vector de dimensión 1) al principio de un vector o en medio del vector

>> a=[1 2 3];
>> b=[4 5 6 7];
>> c=[a b]
c =     1     2     3     4     5     6     7
>> d=[-1 a]
d =    -1     1     2     3
>> e=[d(1:2) -5 d(3:4)]
e =    -1     1    -5     2     3

Elimina elementos de un vector

Se pueden eliminar elementos de un vector

>> e
e =    -1     1    -5     2     3
>> e(2:4)=[]
e =    -1     3

Más adelante veremos como se accede a los elementos de un vector mediante los operadores relacionales

Operaciones con vectores

Suma de un escalar y un vector

>> x=[1,2,3];
>> x+5
ans =     6     7     8

Producto de un escalar por un vector

El producto de un vector u por un escalar λ es otro vector v de la misma dirección, se multiplica cada elemento por el escalar

$v = λ \cdot u = [λ u_{1} λ u_{2} .... λ u_{n}]$

>> u=[1,2,3];
>> u*3
ans =     3     6     9

Se pueden realizar más operaciones con un vector, por ejemplo calcular la raíz cuadrada de un conjunto de datos

>> x=[4 9 16 25];
>> u=sqrt(x)
u =     2     3     4     5
>> 3*u-2
ans =     4     7    10    13

Suma de dos vectores

Los vectores con el mismo número de elementos se pueden sumar o restar.

$\begin{array}{l} u = [u_{1} u_{2} .... u_{n}] v = [v_{1} v_{2} .... v_{n}] \\ u + v = [u_{1} + v_{1} u_{2} + v_{2} .... u_{n} + v_{n}] \end{array}$

>> u=[1,2,3];
>> v=[4,5,6];
>> u+v
ans =     5     7     9

El polinomio p₁=x⁴+3x³-2x²+x-2 se representa por el vector p₁=[1,3,-2,1,-2]. El polinomio p₂=5x²-2x+1 se representa por el vector p₂=[5,-2,1]

No podemos sumar estos dos polinomios ya que los vectores p₁ y p₂ no tienen la misma longitud. Para hacerlos de la misma longitud insertamos a la izquierda los ceros necesarios en el vector que tiene menos elementos.

>> p1=[1,3,-2,1,-2]
p1 =     1     3    -2     1    -2
>> p2=[5,-2,1];
>> p2=[zeros(1,length(p1)-length(p2)),p2]
p2 =     0     0     5    -2     1
>> s=p1+p2
s =      1     3     3    -1    -1

Producto escalar de dos vectores

$\begin{array}{l} u \cdot v = u \cdot v \cdot \cos θ \\ u \cdot v = u_{1} v_{1} + u_{2} v_{2} + .... + u_{n} v_{n} \end{array}$

El producto escalar se obtiene multiplicando el vector fila u por el vector columna v

$(\begin{matrix} u_{1} & u_{2} & ... & u_{n} \end{matrix}) (\begin{matrix} v_{1} \\ v_{2} \\ ... \\ v_{n} \end{matrix}) = u_{1} v_{1} + u_{2} v_{2} + ... + u_{n} v_{n}$

MATLAB dispone de la función dot(u,v) para calcular el producto escalar de dos vectores u y v.

>> u = [5 6 7];
>> v = [4 3 2];
>> dot(u,v)
ans =    52
>> u*v'
ans =    52

Cuando el vector u y v coinciden, calculamos el módulo del vector u.

$u \cdot u = u^{2} = u_{1}^{2} + u_{2}^{2} + .... + u_{n}^{2}$

MATLAB dispone de la función norm que calcula el módulo de un vector.

>> u = [5 6 7];
>> norm(u)
ans =   10.4881
>> sqrt(u*u')
ans =   10.4881

A partir de la definición del producto escalar podemos calcular el ángulo entre los vectores u y v

$\cos θ = \frac{u_{1} \cdot v_{1} + u_{2} v_{2} + .... + u_{n} v_{n}}{u \cdot v}$

Escribimos la ventana de comandos

>> u = [5 6 7];
>> v = [4 3 2];
>> ang=acosd(dot(u,v)/(norm(u)*norm(v))
ang = 22.9745

Dos vectores u y v son perpendiculares si el producto escalar es cero.

La proyección de un vector u a lo largo de la dirección del vector v se calcula del siguiente modo: se multiplica escalarmente el vector u por el vector unitario v/v cuya dirección y sentido son los del vector v.

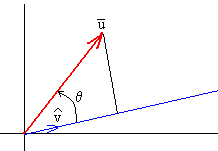
$u_{v} = u \cos θ = u \cdot \frac{v}{v} = \frac{u_{1} \cdot v_{1} + u_{2} v_{2} + .... + u_{n} v_{n}}{v}$

Por ejemplo, el ángulo que forma el vector u con el eje Z se calcula

$\begin{array}{l} u = u_{x} \hat{i} + u_{y} \hat{j} + u_{z} \hat{k} \\ \cos θ = \frac{u_{z}}{u} \end{array}$

Otras formas de crear vectores

En MATLAB hay otras formas alternativas de crear un vector, que como veremos son muy útiles para el cálculo y representación gráfica de funciones.

Para crear un vector con espaciado constante especificando el primer término, x_i, el último término x_f y el número de términos, n llamamos a la función linspace

vector=linspace(xi,xf,n)

>> x=linspace(0,6,5)
x = 0 1.5000  3.0000 4.5000 6.0000

El espaciado constante entre dos valores consecutivos Δx es

$Δ x = \frac{x_{f} - x_{i}}{n - 1}$

Por lo que son equivalentes los vectores definidos por

>> x=0:2:20
>> x=linspace(0,20,11)

Creamos una tabla de valores de la función seno en el intervalo (0, 2π) del siguiente modo:

>> x=0:pi/5:2*pi
x =0 0.6283 1.2566 1.8850 2.5133 3.1416 3.7699 4.3982 5.0265 5.6549 6.2832
>> y=sin(x)
y =0 0.5878 0.9511 0.9511 0.5878 0.0000 -0.5878 -0.9511 -0.9511 -0.5878 -0.0000

Creamos una tabla de logaritmos de la siguiente forma

>> x=(1:0.1:1.5)'; %vector columna
>> logs=[x log10(x)]
logs =
    1.0000         0
    1.1000    0.0414
    1.2000    0.0792
    1.3000    0.1139
    1.4000    0.1461
    1.5000    0.1761

La función logspace es similar a linspace pero genera un conjunto de elementos espaciados logarítmicamente. Por ejemplo, para crear el vector x=[10,100,1000,10000] escribimos

>> x=logspace(1,4,4)
x =          10         100        1000       10000

Operaciones elemento a elemento

Existen muchas situaciones en las que se requieren operaciones elemento a elemento similares a las que se lleva a cabo con la suma o la diferencia de dos vectores de las mismas dimensiones

Sean dos vectores a=[a₁ a₂ a₃] y b=[b₁ b₂ b₃]

Las operaciones de multiplicación, división y exponenciación elemento a elemento de dos vectores a y b se definen del siguiente modo:

$\begin{array}{l} a . * b = [a_{1} b_{1} a_{2} b_{2} a_{3} b_{3}] \\ a . / b = [a_{1} / b_{1} a_{2} / b_{2} a_{3} / b_{3}] \\ a .^b = [{(a_{1})}^{b_{1}} {(a_{2})}^{b_{2}} {(a_{3})}^{b_{3}}] \end{array}$

>> u=[1,2,3];
>> v=[4,5,6];
>> u.*v
ans =     4    10    18

Evaluamos una función y=f(x) cuando le proporcionamos el valor de la variable x.

>> x=2;
>> y=2*x^2-3
y =     5

En MATLAB, podemos utilizar las operaciones elemento a elemento para evaluar una función para un conjunto de valores de la variable x y esto nos va a ser de mucha utilidad en las representaciones gráficas.

>> x=[0,1,-1,2,-3,4];
>> y=2*x.^2-3
y =    -3    -1    -1     5    15    29

Obtener una tabla de valores de la función $y = \frac{x^{2}}{x^{3} + 1}$ en el intervalo (0.5, 2) tomando un espaciado Δx=0.1

>> x =  0.5:0.1:2;
>> f =  x.^2;
>> g =  x.^3+1;
>> y = f./g

Obtener una tabla de valores de la función y=(2x+3)²(x³+2) en el intervalo (-1, +1) tomando un espaciado Δx=0.1

>> x =  -1:0.1:1;
>> f =  2*x+3;
>> g =  x.^3+2;
>> y = (f.^2).*g

o bien, en una sola línea

>> x=-1:0.1:1;
>> y=((2*x+3).^2).*(x.^3+2)

Funciones que operan con vectores

mean(u)	Valor medio de los elementos del vector u	>> u = [3 7 2 16]; >> mean(A) ans = 7
max(u)	c es el mayor elemento del vector u	>> u = [3 7 2 16 9 5 18 13 0 4]; >> c = max(u) c = 18
min(u)	El más pequeño elemento del vector u	>> u = [3 7 2 16]; >> min(u) ans = 2
sum(u)	Devuelve la suma de todos los elementos del vector	>> u = [3 7 2 16]; >> sum(u) ans = 28
sort(u)	Ordena los elementos del vector en orden ascendente	>> u = [3 7 2 16]; >> sort(u) ans = 2 3 7 16
std(u)	Devuelve la desviación estándar	>> u = [3 7 2 16]; >> std(u) ans = 6.3770
dot(u,v)	Calcula el producto escalar u·v de los vectores u y v	>> u = [5 6 7]; >> v = [4 3 2]; >> dot(u,v) ans = 52
cross(u,v)	Calcula el producto vectorial u×v de los vectores u y v.	>> u = [5 6 7]; >> v = [4 3 2]; >> cross(u,v) ans = -9 18 -9

Suma de los elementos de un vector

La suma sum(u) de los elementos de un vector u es un escalar. La suma acumulada cumsum(u) de un vector u es otro vector s cuyos elementos son s(k) k=1...N

$\begin{array}{l} s = \sum_{n = 1}^{N} x (n) = x (1) + x (2) + .... x (N) \\ s (k) = \sum_{n = 1}^{k} x (n) = x (1) + x (2) + .... x (k) \end{array}$

Producto de los elementos de un vector

El producto prod(u) de los elementos de un vector u es un escalar. El producto acumulado cumprod(u) de un vector u es otro vector p cuyos elementos son p(k) k=1...N

$\begin{array}{l} p = \prod_{n = 1}^{N} x (n) = x (1) \cdot x (2) .... x (N) \\ p (k) = \prod_{n = 1}^{k} x (n) = x (1) \cdot x (2) .... x (k) \end{array}$

Probar que

$\begin{array}{l} \sum_{n = 1}^{N} n = \frac{N (N + 1)}{2} \\ \prod_{n = 1}^{N} n = 1 \cdot 2 \cdot 3... \cdot N = N! \end{array}$

>> s=sum(1:5)
s =    15
>> fact=prod(1:5)
fact =   120
>> cumsum(1:5)
ans =     1     3     6    10    15
>> cumprod(1:5)
ans =     1     2     6    24   120

Calcular el valor de las expresión para N=8.

$\prod_{n = 1}^{N} (1 + \frac{3}{n})$

>> n=1:8;
>> u=1+3./n;
>> p=prod(u)
p =   165

Máximo y mínimo

Para obtener el máximo valor de los elementos de un vector

>>  x=[0,0.38,0.71,0.92,1.00,0.92,0.71,0.38,0];
>> [xmax, nmax]=max(x)
xmax =     1
nmax =     5
>> x(5)
ans =     1

La función max nos devuelve dos datos, el valor máximo xmax y el índice nmax del elemento del vector que guarda el máximo. Vemos que el quinto elemento del vector x guarda el máximo valor 1.0.

fliplr

La función fliplr invierte el sentido de los elementos de un vector

>> b=[4 5 6 7]
b =     4     5     6     7
>> fliplr(b)
ans =     7     6     5     4

Ejercicios

1.-Crear el vector que contenga los números pares entre 10 y cero. Crear un vector que contenga los múltiplos de 3 entre 6 y 36, ambos inclusive.

>> x=10:-2:0
x =    10     8     6     4     2     0
>> x=6:3:36
x =     6     9    12    15    18    21    24    27    30    33    36

2.-Sea el vector u=2:3:18;

Acceder a los tres primeros elementos del vector u
Acceder al segundo, cuarto y sexto elementos del vector u
Acceder al sexto, cuarto y sexto elemento del vector u
Acceder a los tres últimos elementos del vector u
Acceder al primero, tercero y cuarto elementos del vector u

>> u=2:3:18
u =     2     5     8    11    14    17
>> u(1:3)
ans =     2     5     8
>> u(2:2:6)
ans =     5    11    17
>> u(end-2:end)
ans =    11    14    17
>> u([1,3,4])
ans =     2     8    11

3.- Crear una tabla de valores del coseno de los ángulos comprendidos entre 0 y 180, de 30 en 30 grados

ángulo	coseno
0
30
60
...

>> ang=0:30:180;
>> y=cosd(ang);
>> [ang',y']
ans =
         0    1.0000
   30.0000    0.8660
   60.0000    0.5000
   90.0000         0
  120.0000   -0.5000
  150.0000   -0.8660
  180.0000   -1.0000

4. Dado el vector de datos u=[5, 9, 2, 4, 1, 12, 7, 6, 5, 8];

El valor máximo y el índice de dicho elemento en el vector u
El valor mínimo y el índice de dicho elemento en el vector u
La suma de todos los elementos
El producto de todos los elementos
El valor medio
Crear un vector v a partir del u pero con los elementos ordenados en orden ascendente, utilizando la función sort

>> u=[5,9,2,4,1,12,7,6,5,8]
u =
     5     9     2     4     1    12     7     6     5     8
>> [m,k]=max(u)
m =    12
k =     6
>> [m,k]=min(u)
m =     1
k =     5
>> sum(u)
ans =    59
>> prod(u)
ans =     7257600
>> mean(u)
ans =    5.9000
>> v=sort(u)
v =     1     2     4     5     5     6     7     8     9    12

5. Crear una tabla de valores de la función

$y = \frac{x^{2} - 2}{x + 4}$

para los siguientes valores de x: -3, -2, -1, 0, 1, 2, 3

>> x=-3:3;
>> y=(x.^2-2)./(x+4);
>> [x',y']
ans =
   -3.0000    7.0000
   -2.0000    1.0000
   -1.0000   -0.3333
         0   -0.5000
    1.0000   -0.2000
    2.0000    0.3333
    3.0000    1.0000

6. Comprobar que

$\lim_{x \to 0} \frac{\sin x}{x} = 1$

Establecer el formato largo para expresar los números con 15 decimales (format long)
Crear un vector x cuyos elementos son 1,0.1, 0.01,0.001,...y calcular el cociente sin(x)/x. Regresar al formato por defecto( format short)

>> format long
>> n=0:5;
>> x=1./10.^n;
>> y=sin(x)./x;
>> [x',y']
ans =
   1.000000000000000   0.841470984807897
   0.100000000000000   0.998334166468282
   0.010000000000000   0.999983333416666
   0.001000000000000   0.999999833333342
   0.000100000000000   0.999999998333333
   0.000010000000000   0.999999999983333
>> format short

7.-Comprobar que la suma

$\sum_{n = 1}^{\infty} \frac{1}{2^{n}} = 1$

Establecer el formato, 15 decimales (format long). Calcular la suma (a) n=10, (b) n=20, (c) n=40.
Crear el vector n, luego el vector y=1/2ⁿ, y sumar los elementos del vector y con la función sum de MATLAB
Restaurar el formato por defecto

>> format long
>> n=1:10;
>> y=1./2.^n;
>> sum(y)
ans =   0.999023437500000
>> format short

8.- Comprobar que la suma

$\sqrt{12} \sum_{n = 0}^{\infty} \frac{{(- 3)}^{- n}}{2 n + 1} = π$

Calcular la suma (a) n=10, (b) n=20, (c) n=40.

>> format long
>> n=0:10;
>> y=sqrt(12)*(-3).^(-n)./(2*n+1);
>> sum(y)
ans =   3.141593304503082
>> pi
ans =   3.141592653589793
>> format short

9.-Comprobar

$\frac{π}{4} = 1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \frac{1}{9} + ...$

>> n=1:4:10001;
>> sum(1./n-1./(n+2))
ans =    0.7853
>> pi/4
ans =    0.7854

>> n=1:2:10001;
>> sum((-1).^((n-1)/2)./n)
ans =    0.7854