for

El bucle for se empleará cuando conocemos el número de veces que se ejecutará una sentencia o un bloque de sentencias, tal como se indica en la figura. La forma general que adopta la sentencia for es

for x=xi:Δx:xf
    sentencias
end

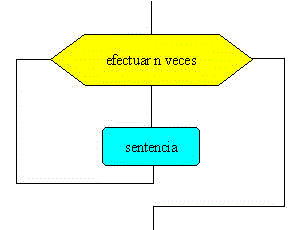
El primer término xi es el valor inicial de la variable x, que controla el número de veces que se ejecutará el bucle. El incremento Δx representa la cantidad que se incrementa la variable x en cada repetición Cuando la variable x sobrepasa el límite xf el bucle termina su ejecución. En la parte derecha de la igualdad tenemos un vector cuyos elementos están igualmente espaciados, sin embargo, esto no tiene que ser siempre así. Después del signo igual se puede poner cualquier vector, como veremos más adelante, x va tomando los valores de los elementos del vector en orden consecutivo.

Escribir un programa que imprima los 10 primeros números enteros empezando por el cero.

for k = 0:10
    disp(k)
end 

Probamos el script en la ventana de comandos

>> prueba
     0
     1
     2... 10

En MATLAB se hace lo mismo creando el vector x del siguiente modo

>> x=0:10
x =     0     1     2     3     4     5     6     7     8     9    10

Escribir un bucle for que imprima los números pares positivos mayores o iguales que 4 y menores o iguales que 20

for k=4:2:20
    disp(k)
end 

En MATLAB se hace lo mismo creando el vector x del siguiente modo

>> x=4:2:20
x =     4     6     8    10    12    14    16    18    20

Escribir un bucle for que imprima los números pares positivos menores o iguales que 20 en orden decreciente

for k=20:-2:0
    disp(k)
end 

Factorial de un número

Escribir un programa que calcule el factorial de un número empleando la sentencia iterativa for.
Definición: el factorial de un número n, n! es el resultado del producto 1·2·3· .... ·(n-1)·n.

Para calcular el factorial del número 4, escribimos el script

n=4;
resultado=1;
for k=1:n
    resultado=k*resultado;
end
fprintf('El factorial de %i es %i\n',n,resultado)

Podemos convertir este conjunto de sentencias en una función. MATLAB dispone de una función denominada factorial que calcula el factorial de un número entero n!, por lo que denominaremos a nuestra función factorial_

>> factorial(4)
ans = 24 

Creamos la función factorial_ que toma un número entero y devuelve el resultado, el factorial de dicho número entero. Guardamos dicha función en un fichero factorial_.m.

function resultado=factorial_(n)
    resultado=1;
    for k=1:n
        resultado=k*resultado;
    end
end

La llamada a la función factorial_ en la ventana de comandos para calcular el factorial de 4, 4!, será

>> factorial_(4)
ans = 24    

MATLAB nos proporciona una forma más rápida de calcular el factorial de un número, utilizando la función producto prod(u) de los elementos de un vector u. Véase al final de la página Vectores

>> n=4;
>> prod(1:n)
ans =    24

El bucle for y los vectores

Mediante un bucle for podemos generar un vector y de ordenadas a partir de un vector x de abscisas. Por ejemplo:

x = 0:0.02:pi;
for k=1:length(x)
    y(k) = sin(x(k));
end 

se puede representar en forma de vectores del siguiente modo

x = 0:0.02:pi
y=sin(x)   

Esta segunda forma es equivalente a la primera pero es más eficiente para MATLAB. En la primera forma, se va incrementando el tamaño del vector y cada vez que se ejecuta el bucle y esto le lleva tiempo a MATLAB, ya que tiene que redimensionar el vector cada vez que un nuevo elemento es calculado y añadido al vector. Una forma de solucionar este problema es reservando anticipadamente memoria para el número de datos que se van a guardar en el vector y.

x = 0:0.02:pi;
%reserva memoria y se asigna 0 a todos los elementos del vector y
y=zeros(length(x),1); 
for k=1:length(x)
    y(k) = sin(x(k));
end 

de este modo el vector y es dimensionado una sola vez, lo que incrementa la eficiencia del programa.

La forma en la que tenemos que escribir un bucle for para que se ejecute en el menor tiempo posible es

y=zeros(1,n); %reservar espacio en memoria para el vector A
for k=1:n
    %sentencias
    y(k)=.....;
end

El comando rand genera números aleatorios uniformente distribuidos en el intervalo comprendido entre 0 y 1, que nos va a permitir inicializar los elementos de una matriz m×n con números aleatorios.

m=3; %filas
n=2; %columnas
x=zeros(m,n); %reserva espacio en memoria para la matriz x de dimensión m×n
for i=1:m
    for j=1:n
        x(i,j)=rand;
    end
end
disp(x)

Probamos el script en la ventana de comandos

    0.2785    0.5469
    0.9575    0.9649
    0.1576    0.9706

MATLAB dispone de un función denominada rand(m,n) que realiza la misma tarea

>> rand(3,2)
ans =
    0.9572    0.1419
    0.4854    0.4218
    0.8003    0.9157

Otras variantes de la función rand son las siguientes:

• rand(n), genera una matriz cuadrada de dimensión n, con números aleatorios entre 0 y 1
• rand(1,n), genera un vector fila de n elementos con números aleatorios entre 0 y 1

Matrices simétricas

Las matrices simétricas son aquellas en las que la matriz A es igual a su traspuesta A^T, es decir, los elementos a_i,j=a_j,i con i≠j. Para crear una matriz simétrica de dimensión n no es necesario inicializar todos los elementos del array, basta con el triángulo superior

n=3;
A=zeros(n);
for i=1:n
    for j=i:n
        A(i,j)=rand;
    end
end

A =
    0.8147    0.9058    0.1270
         0    0.9134    0.6324
         0         0    0.0975

Para crear la matriz simétrica, extraemos la parte triangular superior de la matriz A mediante la función triu

>> A=A+triu(A,1)'
A =
    0.8147    0.9058    0.1270
    0.9058    0.9134    0.6324
    0.1270    0.6324    0.0975
>> A'
ans =
    0.8147    0.9058    0.1270
    0.9058    0.9134    0.6324
    0.1270    0.6324    0.0975

Definición de funciones

Como hemos visto al principio de este apartado, a la función sin de MATLAB se le puede pasar un escalar o un vector. Veamos la diferencia entre las dos definiciones de la función anónima f. Primero, en términos del escalar x

f=@(x) 2*x^2-3*x-2;
x=(0:5)';
y=zeros(length(x),1);
for i=1:length(x)
    y(i)=f(x(i));
end
disp([x,y])

     0    -2
     1    -3
     2     0
     3     7
     4    18
     5    33

Producimos el mismo resultado si definimos la función f en términos del vector x, con un código mucho más simple

f=@(x) 2*x.^2-3*x-2;
x=(0:5)';
y=f(x);
disp([x,y])

Ahora bien, si la función f es constante el resultado de pasarle un vector x no es un vector, sino el valor constante

>> f=@(x) 2;
>> x=(0:5)';
>> f(x)
ans =     2

Vector de funciones

Se puede crear un vector g de tres funciones del siguiente modo

g₁(x)=x
g₂(x)=2x²-1
g₃(x)=4x³-3x

>> g={@(x)x,@(x)2*x.^2-1,@(x)4*x.^3-3*x};
>> g{2}(3)
ans =    17

Se accede a la función de índice 2, g{2} y se calcula el valor de dicha función para x=3, g{2}(3). A dichas funciones vamos a denominar base. Creamos una función f combinación lineal de las funciones base g.

>> a=[1,-1,0.5];
>> f=@(x) a(1)*g{1}(x)+a(2)*g{2}(x)+a(3)*g{3}(x);
>> f(2)
ans =     8

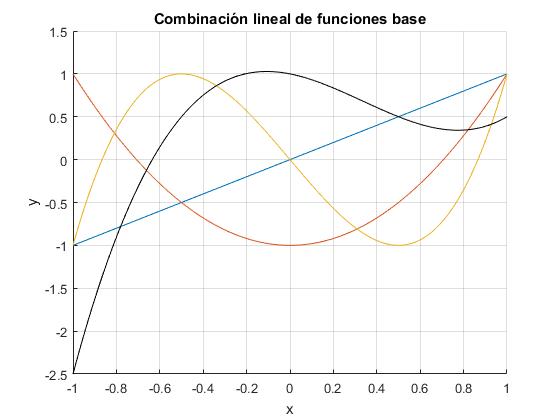
Representamos las funciones base que guardamos en el vector g en color y la función combinación lineal f en color negro. Fijarse en la forma en que que se define la función f en términos de los elementos del vector g

g={@(x)x,@(x)2*x.^2-1,@(x)4*x.^3-3*x};
a=[1,-1,0.5];
f=@(x) a(1)*g{1}(x);
for i=2:length(g)
    f=@(x)(f(x)+a(i)*g{i}(x));
end
hold on
for i=1:length(g)
    fplot(g{i},[-1,1])
end
fplot(f,[-1,1], 'k')
grid on
xlabel('x')
ylabel('y')
title('Combinación lineal de funciones base')

while

A la palabra reservada while le sigue una condición encerrada entre paréntesis. El bloque de sentencias que le siguen se ejecuta siempre que la condición sea verdadera tal como se ve en la figura. La forma general que adopta la sentencia while es:

while condicion
    sentencias
end

Escribir un programa que imprima los primeros 10 primeros números enteros empezando por el cero, empleando la sentencia iterativa while.

k=0;
while k<10
    disp(k)
    k=k+1;
end 

El valor inicial de k es cero, se comprueba la condición (k<10), la cual resulta verdadera. Dentro del bucle, se imprime k, y se incrementa la variable contador k, en una unidad. Cuando k vale 10, la condición (k<10) resulta falsa y el bucle ya no se ejecuta. Si el valor inicial de k fuese 10, no se ejecutaría el bucle. Por tanto, el bucle while no se ejecuta si la condición es falsa.

Factorial de un número

Volvemos a escribir la función factorial_ sustituyendo el bucle for por el bucle while.

function resultado=factorial_(n)
    resultado=1;
    while n>0
        resultado=n*resultado;
        n=n-1;
    end
end

Probamos la nueva versión de la función factorial_ en la ventana de comandos para calcular el factorial de 4, 4!, será

>> factorial_(4)
ans = 24 

El número e

${\displaystyle e=\underset{x\to 0}{\lim }{\left(1+x\right)}^{1/x}}$

Elaboramos un script para calcular el valor aproximado de e, cuando x tiende a cero

format long
x=1;
while x>1e-8
  x=x/10;
  e=(1+x)^(1/x);
  disp([x e]);
end

Corremos el script en la ventana de comandos

   0.100000000000000   2.593742460100002
   0.010000000000000   2.704813829421529
   0.001000000000000   2.716923932235594
   0.000100000000000   2.718145926824926
   0.000010000000000   2.718268237192297
   0.000001000000000   2.718280469095753
   0.000000100000000   2.718281694132081
   0.000000010000000   2.718281798347357
   0.000000001000000   2.718282052011560
>> e
e =   2.718282052011560

break

break es de gran importancia en los bucles, ya que detienen su ejecución cuando se cumple una determinada condición

for k = 0:10 
    if k == 8 
        break 
    end 
    disp(k) 
end 

Consideremos de nuevo el ejemplo del bucle for, que imprime los 10 primeros números enteros, se interrumpe la ejecución del bucle cuando se cumple la condición de que la variable contador k valga 8. El código se leerá: "salir del bucle cuando la variable contador k, sea igual a 8". Como podemos apreciar, la ejecución del bucle finaliza prematuramente. Quizás el lector pueda pensar que esto no es de gran utilidad pues, el código anterior es equivalente a

for k = 0:7
    disp(k)
end

Sin embargo, podemos salir fuera del bucle prematuramente si se cumple alguna condición de finalización.

while 1==1
    %...otras sentencias
    if condicionFinal
        break
    end
end

Como podemos apreciar en esta porción de código, la expresión en el bucle while es siempre verdadera, por tanto, tiene que haber algún mecanismo que nos permita salir del bucle. Si la condición de finalización es verdadera, se sale del bucle, en caso contrario se continua el procesamiento de los datos.

Ejemplos

1.-Desarrollo en serie

El desarrollo en serie de sin(x) es

${\displaystyle \begin{array}{l}\sin (x)\approx x-\frac{1}{3!}{x}^3+\frac{1}{5!}{x}^5-\mathrm{...}\\ \sin (x)=\underset{N\to \infty }{\lim }{\displaystyle \sum _{n=0}^N{(-1)}^n\frac{x^{2n+1}}{(2n+1)!}}\end{array}}$

Comparar el valor dado por la función MATLAB sin(x) con el valor obtenido al sumar un número determinado de términos (5, 10, 15..) del desarrollo en serie para un argumento dado, por ejemplo, x=π/6 (30 grados).

Definir una función denominada serie_sin que admita como parámetros el número n de términos de la serie y el argumento x (radianes) de la función sin.

function resultado=serie_sin(n,x)
    resultado=x;
    signo=-1;
    for i=3:2:2*n-1
        resultado=resultado+signo*x^i/factorial(i);
        signo=-signo;
    end
end

Probamos la función serie_sin en la ventana de comandos

>> format long
>> serie_sin(2, pi/6)
ans = 0.499674179394364
>> serie_sin(5, pi/6)
ans = 0.500000000020280
>> format short
>> sin(pi/6)
ans = 0.5000

Como vemos con muy pocos términos del desarrollo en serie obtenemos el valor 0.5 del seno de 30° o de π/6

Obtenemos el mismo resultado con el siguiente código, que calcula el seno de los ángulos: 30, 60 y 90 con la suma de 10 términos del desarrollo en serie y los compara con el valor que se obtiene a partir de la función sin.

n=0:10;
for x=(30:30:90)*pi/180
    se=sin(x);
    s=sum(((-1).^n).*(x.^(2*n+1))./factorial(2*n+1));
    [se,s]
end

ans =    0.5000    0.5000
ans =    0.8660    0.8660
ans =    1.0000    1.0000

Repetir este ejercicio pero con la función coseno

${\displaystyle \cos (x)=\underset{N\to \infty }{\lim }{\displaystyle \sum _{n=0}^N{(-1)}^n\frac{x^{2n}}{(2n)!}}}$

2.-El número irracional π

Para hallar la longitud de una circunferencia de radio R, primero se calcula el perímetro de un triángulo equilátero (3 lados) inscrito en dicha circunferencia, luego, de un hexágono (6 lados), un dodecágono (12 lados) y así, sucesivamente. El límite de la sucesión de perímetros es precisamente la longitud de la circunferencia 2πR.

Si tomamos una circunferencia de radio unidad, al dividir entre dos los valores de los perímetros iremos obteniendo las sucesivas aproximaciones del número irracional π.

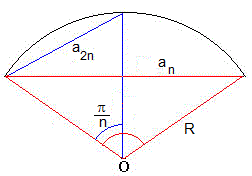
Calculamos la longitud del lado a_n un polígono regular de n lados inscrito en la circunferencia de radio R, (en color rojo).

${\displaystyle a_n=2R\sin \left(\frac{\pi }{n}\right)}$

Del mismo modo, obtenemos la longitud del lado de un polígono regular inscrito de 2n lados (en color azul)

${\displaystyle a_{2n}=2R\sin \left(\frac{\pi }{2n}\right)}$

Teniendo en cuenta que

${\displaystyle \sin \left(\frac{\alpha }{2}\right)=\sqrt{\frac{1-\cos \alpha }{2}}=\sqrt{\frac{1-\sqrt{1-{\sin }^2\alpha }}{2}}}$

Establecemos la relación entre a_n y a_2n y por tanto, entre el perímetro P_n del polígono regular de n lados y el perímetro P_2n del polígono regular de 2n lados.

${\displaystyle P_{2n}=2nR\sqrt{2-\sqrt{4-\frac{P_n^2}{R^2{n}^2}}}}$

Tomando como radio R, la unidad

Para un triángulo, n=3, la longitud del lado es a₃=2sin60°, y el perímetro ${\displaystyle P_3=3\sqrt{3}}$

• Para un hexágono, n=6, la longitud del lado es a₆=2sin30°=1, y el perímetro P₆=6.
• y así, sucesivamente.

Para obtener las sucesivas aproximaciones del número irracional π mediante la fórmula anterior procedemos del siguiente modo:

1. Partimos del valor del perímetro P de un triángulo equilátero inscrito en una circunferencia de radio unidad, el valor de n es 3.
2. Calculamos el perímetro P de un polígono de 2n lados a partir del valor del perímetro de un polígono regular de n lados.
3. El valor obtenido P será el valor del perímetro de un polígono regular de n=2n lados.
4. Se imprime el valor de P dividido entre dos (aproximación de π)
5. Se vuelve al paso 2.

Definimos la función aprox_pi a la que se le pasa el número de iteracciones y devuelve una aproximación del número π. La función no devuelve ningún dato

function aprox_pi(iter)
    perimetro=3*sqrt(3);      
    n=3;    
    for i=1:iter
        perimetro=2*n*sqrt(2.0-sqrt(4.0-(perimetro/n)*(perimetro/n)));
        n=2*n;
        fprintf('%i lados, aproximación de pi: %1.8f\n',n,perimetro/2)
    end
end

Probamos la función aprox_pi en la ventana de comandos

>> aprox_pi(10)
6 lados, aproximación de pi: 3.00000000
12 lados, aproximación de pi: 3.10582854
24 lados, aproximación de pi: 3.13262861
48 lados, aproximación de pi: 3.13935020
96 lados, aproximación de pi: 3.14103195
192 lados, aproximación de pi: 3.14145247
384 lados, aproximación de pi: 3.14155761
768 lados, aproximación de pi: 3.14158389
1536 lados, aproximación de pi: 3.14159046
3072 lados, aproximación de pi: 3.14159211
>> format long
>> pi
ans = 3.141592653589793 
>> format short

3.-Ordenar una lista de números

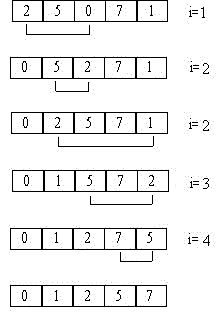
Para ordenar una lista de números emplearemos el método de la burbuja, un método tan simple como poco eficaz. Se compara el primer elemento, índice 0, con todos los demás elementos de la lista, si el primer elemento es mayor que el elemento j, se intercambian sus valores, siguiendo el procedimiento explicado en la figura. Se continua este procedimiento con todos los elementos del array menos el último. La figura explica de forma gráfica este procedimiento.

Crear una función denominada ordenar que devuelva un vector ordenado en orden ascendente cuando se le pasa un vector de datos desordenado

function x=ordenar(x)
    n=length(x);
    for i=1:n
        for j=i+1:n
            if x(i)>x(j)
                aux=x(j);
                x(j)=x(i);
                x(i)=aux;
            end
        end
    end
end

Llamamos a la función ordenar y le pasamos el vector de datos desordenados: 1.65 1.82 1.72 1.75 1.73 1.85 1.90 1.74 1.76 1.77

>> ordenar([1.65 1.82 1.72 1.75 1.73 1.85 1.90 1.74 1.76 1.77])
ans = 1.6500 1.7200 1.7300 1.7400 1.7500 1.7600 1.7700 1.8200 1.8500 1.9000

MATLAB dispone de una función denominada sort que realiza la misma tarea

>> sort([1.65 1.82 1.72 1.75 1.73 1.85 1.90 1.74 1.76 1.77])

4.-Números primos

Los números primos tienen la siguiente característica: un número primo es solamente divisible por sí mismo y por la unidad, por tanto, un número primo no puede ser par excepto el 2. Para saber si un número impar es primo, dividimos dicho número por todos los números impares comprendidos entre 3 y la mitad de dicho número. Por ejemplo, para saber si 13 es un número primo basta dividirlo por 3 y 5. Para saber si 25 es número primo se divide entre 3, 5, 7, 9 y 11. Si el resto de la división es cero, el número no es primo.

Crear una función denominada es_primo que devuelva un cero (false) si no es primo y un uno (true) si es primo, cuando se le pasa un número entero n mayor que 3.

function bPrimo=es_primo(n)       
    bPrimo=1;   
    for i=3:2:n/2
        if rem(n,i)==0 
            bPrimo=0;
            break;
          end
    end
end

Probamos la función es_primo en la ventana de comandos

>> es_primo(13)
ans = 1
>> es_primo(10)
ans = 0

MATLAB dispone de la función que realiza la misma tarea, isprime(n) que nos dice si un número es o no primo. Otra función denominada primes(n), devuelve los números primos hasta e incluyendo el argumento

>> isprime(13)
ans = 1
>> isprime(10)
ans = 0
>> primes(20)
ans = 2  3  5  7  11  13  17  19

Crear una función denominada primos que imprima los números primos menores que n según los va calculando, la función no devuelve ningún dato

function primos(n)
    disp(2);
    for i=3:2:n;
        if es_primo(i)
            disp(i)
        end
    end
end

Probamos la función primos en la ventana de comandos

>> primos(20)
     2
     3
     5
     7
    11
    13
    17
    19 

Podemos definir una función primos que devuelva un vector cuyos elementos sean los números primos

5.-Simplificar una fracción

Para simplificar una fracción primero hay que hallar el máximo común divisor del numerador y del denominador. Para ello se emplea el algoritmo de Euclides, cuyo funcionamiento se muestra en el siguiente ejemplo. Sea u=1260 y v=231,

En la primera iteración, se halla el resto r de dividir el primero u entre el segundo v. Se asigna a u el divisor v, y se asigna a v el resto r.

En la segunda iteracción, se halla el resto r de dividir u entre v. Se asigna a u el divisor v, y se asigna a v el resto r.

Se repite el proceso hasta que el resto r sea cero. El máximo común divisor será el último valor de v.

1260=231×5+105
231=105×2+21
105=21×5+0

el máximo común divisor es 21.

A continuación, definimos la función simplificar, de modo que al aplicarlo sobre una fracción, dicha fracción se reduzca a la fracción equivalente más simple. Para ello, se divide numerador y denominador por el máximo común divisor de ambos números y devuelve la fracción simplificada.

function [num,den]=simplificar(numerador, denominador)
    u=abs(numerador);
    v=abs(denominador);
    if v==0
        res=u;
    else
        while v~=0
            r=rem(u,v);
            u=v;
            v=r;
        end
        res=u;
    end  
    num=numerador/res;
    den=denominador/res;
 end

Si queremos calcular la fracción equivalente a 12/18 más simple, escribimos

>> [num,den]=simplificar(12,18)
num = 2
den = 3

nos da la fracción 2/3

La función MATLAB gcd devuelve el máximo común divisor de dos números x e y, o la unidad si son primos

>> mcd=gcd(12,18)
>> 12/mcd,18/mcd

Obtenemos la fracción 2/3

En el primer capítulo Cálculos aritméticos, hemos visto que MATLAB sabe operar con fracciones y devuelve la fracción más simple.