Una matriz A de m filas y n columnas o de dimensión m×n se representa por

${\displaystyle A=\left[\begin{array}{cccc}{a}_{11}& a_{12}& \mathrm{...}& a_{1n}\\ a_{21}& a_{22}& \mathrm{...}& a_{2n}\\ \mathrm{...}& \mathrm{...}& \mathrm{...}& \mathrm{...}\\ a_{m1}& a_{m2}& \mathrm{...}& a_{mn}\end{array}\right]}$

Para acceder a un elemento situado en la fila i y en la columna j, A_ij, se escribe A(i,j). La función size devuelve dos números que corresponden a las dimensiones de la matriz.

La matriz traspuesta A' de la matriz A consiste en intercambiar filas por columnas: La primera columna de la matriz A es la primera fila de la matriz traspuesta A', la segunda columna de la matriz A se convierte en segunda fila de la matriz A', y así sucesivamente. La dimensión de la matriz tarspuesta A' es n×m, es decir n filas y m columnas

${\displaystyle A\text{'}=\left[\begin{array}{cccc}{a}_{11}& a_{21}& \mathrm{...}& a_{m1}\\ a_{12}& a_{22}& \mathrm{...}& a_{m2}\\ \mathrm{...}& \mathrm{...}& \mathrm{...}& \mathrm{...}\\ a_{1n}& a_{2n}& \mathrm{...}& a_{mn}\end{array}\right]}$

Creación de una matriz

Se crea una matriz de 3×2, y asignar a la variable A de dos formas distintas

>> A=[1 2 3
4 5 6];
>> A=[1 2 3; 4 5 6]
A =
     1     2     3
     4     5     6
>> A(2,2) %accede al elemento situado en la fila 2 columna 2
ans = 5
>> size(A)  %dimensiones de la matriz A (2 filas, 3 columnas)
ans = 2     3
>> B=A' % B es la matriz traspuesta de A
B =
     1     4
     2     5
     3     6
>> size(B)
ans =     3     2

La función size se utiliza para obtener las dimensiones de una matriz, mientras que la función length, se utiliza para conocer el número de elementos de un vector.

Haciendo doble-clic en en nombre de la variable A en la ventana Workspace o bien, seleccionado la variable en el menú Open variable, se muestra el contenido de la matriz A, en celdas que que contienen los elementos de la matriz que podemos modificar, tal como se muestra en la figura

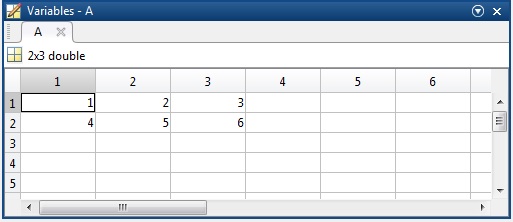
Creamos matrices a partir de vectores o a partir de otras matrices

>> x1=[1,2,3]; %vectores fila
>> x2=[4,5,6]; 
>> A=[x1;x2]
A =
     1     2     3
     4     5     6
>> x1=[1;2;3]; %vectores columna 
>> x2=[4;5;6];
>> A=[x1,x2]
A =
     1     4
     2     5
     3     6

>> X=[1,2,3;4,5,6]
X =
     1     2     3
     4     5     6
>> Y=[7,8,9;10,11,12;13,14,15]
Y =
     7     8     9
    10    11    12
    13    14    15
>> A=[X;Y]
A =
     1     2     3
     4     5     6
     7     8     9
    10    11    12
    13    14    15

La funcion repmat crea una matriz B compuesta de la repetición de n×m copias de A.

>>  A=[1,2;3,4]
A =
     1     2
     3     4
>> B=repmat(A,3,2)
B =
     1     2     1     2
     3     4     3     4
     1     2     1     2
     3     4     3     4
     1     2     1     2
     3     4     3     4

La función meshgrid, crea dos matrices U y V de la misma dimensión a partir de dos vectores u=1:4 y v=5:7

>> [U,V]=meshgrid(1:4,5:7)
U =
     1     2     3     4
     1     2     3     4
     1     2     3     4
V =
     5     5     5     5
     6     6     6     6
     7     7     7     7

Las matrices U y V se pueden generar alternativamente con la función repmat

>> U=repmat(1:4,3,1)
U =
     1     2     3     4
     1     2     3     4
     1     2     3     4
>> V=repmat((5:7)',1,4)
V =
     5     5     5     5
     6     6     6     6
     7     7     7     7

Vamos a crear la siguiente matriz cuadrada de dimensión N=4

${\displaystyle x_{ij}=\frac{1}{i+j-1}i,j=\mathrm{1,2...}N}$

>> [I,J]=meshgrid(1:4);
>> X=1./(I+J-1)
X =
    1.0000    0.5000    0.3333    0.2500
    0.5000    0.3333    0.2500    0.2000
    0.3333    0.2500    0.2000    0.1667
    0.2500    0.2000    0.1667    0.1429

La función meshgrid, se utilizará para calcular y dibujar superficies tridimensionales z=f(x,y)

Una matriz se puede convertir en un vector columna

>> A=[1,2,3;4,5,6];
>> X=A(:)
X =
     1
     4
     2
     5
     3
     6

Un vector se puede convertir en una matriz diagonal mediante diag.

>> x=[1,2,3];
>> A=diag(x)
A =
     1     0     0
     0     2     0
     0     0     3

Creamos una matriz de 3×4 con números enteros aleatorios comprendidos entre -10 y 10

>> A=randi([-10,10],3,4)
A =
     4    -2     4   -10
     5     3   -10    -8
     5    -7    -5     7

Estos doce valores los reorganizamos en una matriz de 2 filas y 6 columnas, mediante la función reshape

>> reshape(A,2,6)
ans =
     4     5     3     4    -5    -8
     5    -2    -7   -10   -10     7

La función flipud invierte el orden de las filas de la matriz A

>> flipud(A)
ans =
     5    -7    -5     7
     5     3   -10    -8
     4    -2     4   -10

La función fliplr invierte el orden de las columnas

>> fliplr(A)
ans =
   -10     4    -2     4
    -8   -10     3     5
     7    -5    -7     5

Matrices predefinidas

• La función zeros(m,n) crea una matriz de dimensión m×n cuyos elementos son todos ceros
• La función ones(m,n) crea una matriz de dimensión m×n cuyos elementos son todos unos
• La función eye(n) crea una matriz cuadrada de dimensión n×n en la cual, los elementos de la diagonal son unos y el resto de los elementos son ceros, es decir, crea la matriz identidad de dimensión n.

Por ejemplo, zeros(n) reserva espacio para una matriz cuadrada de dimensión n×n. Lo mismo ocurre con ones(n)

>> y=zeros(3)
y =
     0     0     0
     0     0     0
     0     0     0
>> y=zeros(3,1)
y =
     0
     0
     0
>> eye(3)
ans =
     1     0     0
     0     1     0
     0     0     1

Acceso a los elementos de una matriz

Existen también varias formas de acceder a más de un elemento de una matriz mediante el operador dos puntos :. Sea la matriz A.

${\displaystyle \left(\begin{array}{cccc}1& 2& 3& 4\\ 5& 6& 7& 8\\ 9& 10& 11& 12\\ 13& 14& 15& 16\end{array}\right)}$

• A(:,2) se accede a todos los elementos de la columna 2
• A(:,end) se accede a todos los elementos de la última columna
• A(3,:) se accede a todos los elementos de la fila 3
• A(:,2:4) se accede a todos los elementos de las columnas 2, 3 y 4
• A(2:4,:) se accede a todos los elementos de las filas 2, 3 y 4
• A(1:3,2:4) se refiere a la submatriz de filas 1, 2 y 3 y de columnas 2, 3 y 4

>> A=[1 2 3 4; 5 6 7 8; 9 10 11 12; 13 14 15 16]
A =
     1     2     3     4
     5     6     7     8
     9    10    11    12
    13    14    15    16

>> A(:,2)
ans =
     2
     6
    10
    14

>> A(3,:)
ans =
     9    10    11    12

>> A(:,2:4)
ans =
     2     3     4
     6     7     8
    10    11    12
    14    15    16

>> A(2:4,:)
ans =
     5     6     7     8
     9    10    11    12
    13    14    15    16

>> A(1:3,2:4)
ans =
     2     3     4
     6     7     8
    10    11    12

Para acceder a los elementos de la matriz sobreados en la figura escribiremos

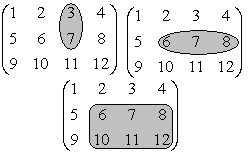
>> A=[1,2,3,4;5,6,7,8;9,10,11,12];
>> A([1,2],3)
ans =
     3
     7
>> A(2,[2,3,4])
ans =
     6     7     8
>> A([2,3],2:4)
ans =
     6     7     8
    10    11    12

Eliminar elementos de una matriz

Se pueden eliminar elementos a una matriz A y luego volverlos a añadir

>> A=[1 2 3 4; 5 6 7 8; 9 10 11 12; 13 14 15 16];
>> A(4,:)=[]
A =
     1     2     3     4
     5     6     7     8
     9    10    11    12

>> A(4,:)=13:16
A =
     1     2     3     4
     5     6     7     8
     9    10    11    12
    13    14    15    16

Se puede crear una matriz a partir de vectores columna, por ejemplo para crear una tabla de valores (abscisa, ordenada) de una función. Se puede calcular la suma de valores, el valor máximo, mínimo, etc de cada columna, tal como lo hicimos con los vectores en la página anterior.

>> x=0:5; %vector fila
>> y=3*x.^2-5; %vector fila
>> tabla=[x' y']
tabla =
     0    -5
     1    -2
     2     7
     3    22
     4    43
     5    70
>> size(tabla) %matriz de 6 filas y 2 columnas
ans =     6     2
>> max(tabla(:,2))
ans =    70
>> min(tabla(:,2))
ans =    -5
>> sum(tabla(:,2))
ans =   135

Creamos una tabla de cuadrados del número entero n, n² y de potencias de 2 elevado a la n, 2ⁿ del siguiente modo

>> n=[0:5]';
>> potencias=[n n.^2 2.^n]
potencias =
     0     0     1
     1     1     2
     2     4     4
     3     9     8
     4    16    16
     5    25    32

En la página titulada Valores y vectores propios tendremos ocasión de practicar con matrices, vectores, extraer una matriz o un vector de otra matriz, crear una matriz a partir de vectores, etc

Ordenar los elementos de una matriz

MATLAB dispone de una función denominada sort para ordenar los elementos de un vector

>> sort([1.65 1.82 1.72 1.75 1.73 1.85 1.90 1.74 1.76 1.77])
ans = 1.6500 1.7200 1.7300 1.7400 1.7500 1.7600 1.7700 1.8200 1.8500 1.9000

En el caso de tablas bidimensionales o multidimensionales, MATLAB dispone de la función sortrows que realiza esta tarea. Por ejemplo, queremos ordenar la siguiente tabla primero por días y después por temperaturas

>> a=[15 21; 3 32; 17 15; 21 19; 8 35]
a =
    15    21
     3    32
    17    15
    21    19
     8    35
>> sortrows(a,1)
ans =
     3    32
     8    35
    15    21
    17    15
    21    19
>> sortrows(a,2)
ans =
    17    15
    21    19
    15    21
     3    32
     8    35

Operaciones con matrices

Suma de matrices de la misma dimensión

${\displaystyle \begin{array}{l}\end{array}}$ ${\displaystyle \begin{array}{l}A=\left[\begin{array}{ccc}{a}_{11}& a_{12}& a_{13}\\ a_{21}& a_{22}& a_{23}\end{array}\right]B=\left[\begin{array}{ccc}{b}_{11}& b_{12}& b_{13}\\ b_{21}& b_{22}& b_{23}\end{array}\right]\\ A+B=\left[\begin{array}{ccc}(a_{11}+b_{11})& (a_{12}+b_{12})& (a_{13}+b_{13})\\ (a_{21}+b_{21})& (a_{22}+b_{22})& (a_{23}+b_{23})\end{array}\right]\end{array}}$

Como ejercicio se sugiere comprobar el resultado de la suma de dos matrices

Producto de dos matrices

Se pueden multiplicar matrices de dimensiones (m, k) ×(k, n) para obtener una matriz de dimensión (m, n).

${\displaystyle \begin{array}{l}A=\left[\begin{array}{ccc}{a}_{11}& a_{12}& a_{13}\\ a_{21}& a_{22}& a_{23}\end{array}\right]B=\left[\begin{array}{cc}{b}_{11}& b_{12}\\ b_{21}& b_{22}\\ b_{31}& b_{32}\end{array}\right]\\ A*B=\left[\begin{array}{cc}(a_{11}{b}_{11}+a_{12}{b}_{21}+a_{13}{b}_{31})& (a_{11}{b}_{12}+a_{12}{b}_{22}+a_{13}{b}_{32})\\ (a_{21}{b}_{11}+a_{22}{b}_{21}+a_{23}{b}_{31})& (a_{21}{b}_{12}+a_{22}{b}_{22}+a_{23}{b}_{32})\end{array}\right]\end{array}}$

>> A=[1 2 3;4 5 6]
A =
     1     2     3
     4     5     6
>> B=[1 2; 3 4; 5 6]
B =
     1     2
     3     4
     5     6
>> A*B
ans =
    22    28
    49    64

El producto de un vector columa m×1 por un vector fila 1×m, del mismo número de elementos m nos da una matriz cuadrada de dimensión m×m.

Producto de un escalar por una matriz

Cuando una matriz se multiplica por un número, cada elemento de la matriz se multiplica por dicho número

${\displaystyle \begin{array}{l}A=\left[\begin{array}{ccc}{a}_{11}& a_{12}& a_{13}\\ a_{21}& a_{21}& a_{23}\end{array}\right]\\ k*A=\left[\begin{array}{ccc}k·a_{11}& k·a_{12}& k·a_{13}\\ k·a_{21}& k·a_{21}& k·a_{23}\end{array}\right]\end{array}}$

La operación kA es commutativa, se obtiene el mismo resultado haciendo el producto Ak

Operaciones elemento a elemento

Existen muchas situaciones en las que se requieren operaciones elemento a elemento similares a las que se lleva a cabo con la suma o la diferencia de dos matrices de las mismas dimensiones.

${\displaystyle \begin{array}{l}A=\left[\begin{array}{ccc}{a}_{11}& a_{12}& a_{13}\\ a_{21}& a_{22}& a_{23}\\ a_{31}& a_{32}& a_{33}\end{array}\right]B=\left[\begin{array}{ccc}{b}_{11}& b_{12}& b_{13}\\ b_{21}& b_{22}& b_{23}\\ b_{31}& b_{32}& b_{33}\end{array}\right]\\ A.*B=\left[\begin{array}{ccc}{a}_{11}{b}_{11}& a_{12}{b}_{12}& a_{13}{b}_{13}\\ a_{21}{b}_{21}& a_{22}{b}_{22}& a_{23}{b}_{23}\\ a_{31}{b}_{31}& a_{32}{b}_{32}& a_{33}{b}_{33}\end{array}\right]\\ A./B=\left[\begin{array}{ccc}{a}_{11}/b_{11}& a_{12}/b_{12}& a_{13}/b_{13}\\ a_{21}/b_{21}& a_{22}/b_{22}& a_{23}/b_{23}\\ a_{31}/b_{31}& a_{32}/b_{32}& a_{33}/b_{33}\end{array}\right]\\ A.^n=\left[\begin{array}{ccc}{(a_{11})}^n& {(a_{12})}^n& {(a_{13})}^n\\ {(a_{21})}^n& {(a_{22})}^n& {(a_{23})}^n\\ {(a_{31})}^n& {(a_{32})}^n& {(a_{33})}^n\end{array}\right]\end{array}}$

>> A=[1,2,-4;7,0,5];
>> B=[-6,12,-5;-2,16,15];
>> A.*B
ans =
    -6    24    20
   -14     0    75
>> A.^2
ans =
     1     4    16
    49     0    25
>> A./B
ans =
   -0.1667    0.1667    0.8000
   -3.5000         0    0.3333

Ejercicios

1.-Crear estas dos matrices A y B sin inicializar cada elemento de la matriz, en una sola línea en la ventana de comandos

${\displaystyle \left(\begin{array}{ccc}1& 0& -6\\ 2& 0& -4\\ 3& 0& -2\\ 4& 0& 0\\ 5& 0& 2\end{array}\right)}$

${\displaystyle \left(\begin{array}{cccccc}1& 3& 5& 7& 9& 11\\ 0& 5& 10& 15& 20& 25\\ 10& 20& 30& 40& 50& 60\\ -6& -4& -2& 0& 2& 4\end{array}\right)}$

• Eliminar la última fila de la primera matriz y la tercera columna de la segunda matriz

>> A=[(1:5)',zeros(5,1),(-6:2:2)']
A =
     1     0    -6
     2     0    -4
     3     0    -2
     4     0     0
     5     0     2
>> B=[1:2:11;0:5:25;10:10:60;-6:2:4]
B =
     1     3     5     7     9    11
     0     5    10    15    20    25
    10    20    30    40    50    60
    -6    -4    -2     0     2     4
>> A(end,:)=[]
A =
     1     3     5     7     9    11
     0     5    10    15    20    25
    10    20    30    40    50    60
>> B(:,3)=[]
B =
     1     3     7     9    11
     0     5    15    20    25
    10    20    40    50    60
    -6    -4     0     2     4

2.-Crear la matriz B de 5×6 a partir de un vector A de 30 elementos utilizando el comando reshape, y acceder a los elementos marcados en color rojo

Nota: reshape(A,m,n) crea una matriz m×n a partir de los elementos de la matriz A que debe tener m·n elementos.

>> A=1:30;
>> B=reshape(A,5,6)
B =
     1     6    11    16    21    26
     2     7    12    17    22    27
     3     8    13    18    23    28
     4     9    14    19    24    29
     5    10    15    20    25    30
>> B([3,4,5],[4,5])
ans =
    18    23
    19    24
    20    25
>> B(2:4,3:5)
ans =
    12    17    22
    13    18    23
    14    19    24
>> B(2:end,end)
ans =
    27
    28
    29
    30
>> B(end,3:5)
ans =
    15    20    25

3. Sea la matriz

${\displaystyle \left(\begin{array}{ccccc}0& 2& 3& 4& 2\\ -2& 3& -1& 5& 1\\ 0& 2& -4& -3& 1\end{array}\right)}$

• Crear un vector columna de nueve elementos que contenga los elementos de la primera, tercera y cuarta columna
• Crear un vector fila de ocho elementos, que contenga los elementos de la sugunda fila y de la tercera columna
• Crear un vector fila de cinco elementos que contenga los dos últimos elementos de la última columna y los tres primeros elementos de la primera fila.

>> A=[0,2,3,4,2;-2,3,-1,5,1;0,2,-4,-3,1]
A =
     0     2     3     4     2
    -2     3    -1     5     1
     0     2    -4    -3     1
>> u=[A(:,1);A(:,3);A(:,4)]
u =
     0
    -2
     0
     3
    -1
    -4
     4
     5
    -3
>> u=[A(2,:),A(:,3)']
u =
    -2     3    -1     5     1     3    -1    -4
>> u=[A(end-1:end,end)',A(1,1:3)]
u =     1     1     0     2     3

4.-Sean las matrices

${\displaystyle A=\left(\begin{array}{ccc}1& 0& -1\\ 4& -2& -3\end{array}\right)B=\left(\begin{array}{ccc}1& -2& 3\\ 1& -1& 2\end{array}\right)}$

Realizar las siguientes operaciones

• A*B^T(el superíndice T indica traspuesta)
• A^T*B
• A.*B (producto elemento a elemento)
• A./B

>> A=[1,0,-1;4,-2,-3]
A =
     1     0    -1
     4    -2    -3
>> B=[1,-2,3;1,-1,2]
B =
     1    -2     3
     1    -1     2
>> A*B'
ans =
    -2    -1
    -1     0
>> A'*B
ans =
     5    -6    11
    -2     2    -4
    -4     5    -9
>> A.*B
ans =
     1     0    -3
     4     2    -6
>> A./B
ans =
    1.0000         0   -0.3333
    4.0000    2.0000   -1.5000

5.- Sean las matrices

${\displaystyle A=\left(\begin{array}{ccc}2& 4& -1\\ 3& 1& -5\\ 0& 1& 4\end{array}\right)B=\left(\begin{array}{ccc}-2& 5& 0\\ -3& 2& 7\\ -1& 6& 9\end{array}\right)C=\left(\begin{array}{ccc}0& 3& 5\\ 2& 1& 0\\ 4& 6& -3\end{array}\right)}$

Comprobar si son verdaderas o falsas estas afirmaciones:

• A+(B+C)= (A+B)+C, propiedad asociativa
• 2(A+B)=2A+2B
• A*(B+C)=A*B+A*C, propiedad distributiva
• A*B=B*A, propiedad conmutativa
• (A*B)^T=B^T*A^T
• (A*B)*C=A*(B*C)
• (A+B)^T=A^T+B^T