Operadores relacionales
La comparación, 8>4 (ocho mayor que cuatro) es verdadera, se representa por el valor 1, en cambio, 8<4 (ocho menor que cuatro) es falsa, se representa por el valor 0. En la primera columna de la tabla, se dan los símbolos de los operadores relacionales, el la segunda, el nombre de dichos operadores, y a continuación su significado mediante un ejemplo.
| Operador | Nombre | Ejemplo | Significado |
|---|---|---|---|
< |
menor que |
a<b |
a es menor que b |
> |
mayor que |
a>b |
a es mayor que b |
== |
igual a |
a==b |
a es igual a b |
~= |
no igual a |
a~=b |
a no es igual a b |
<= |
menor que o igual a |
a<=5 |
a es menor que o igual a b |
>= |
mayor que o igual a |
a>=b |
a es menor que o igual a b |
MATLAB no dispone del tipo de dato boolean (true, false), si la expresión es verdadera da como resultado 1, si es falsa da como resultado 0.
>> 5>4 ans = 1 >> 5>6 ans = 0
El carácter ~ se obtiene manteniendo pulsada la tecla Alt y pulsando en el teclado numérico las teclas 126. Corresponde al carácter ASCII decimal 126.
Se debe tener especial cuidado en no confundir el operador asignación con el operador relacional igual a. Las asignaciones se realizan con el símbolo =, las comparaciones con ==.
Si dos escalares a y b se comparan el resultado puede ser verdadero (1) o falso (0) de acuerdo con la tabla anterior.
Si a y b son vectores de la misma dimensión, se compara cada elemento a(i) con b(i) el resultado es que el elemento (i) del vector resultado u(i) puede contener un 1 ó 0.
Si se comparan dos matrices (de la mismas dimensiones) la comparación se hace elemento a elemento y el resultado es otra matriz de la misma dimensión con unos y ceros de acuerdo con el resultado de la comparación.
>> a=[15 6 9 4 11 7 14]
a= 15 6 9 4 11 7 14
>> b=[8 20 9 2 19 7 10]
b= 8 20 9 2 19 7 10
>> u=a>=b
u =
1 0 1 1 0 1 1
Un vector o una matriz como u que contiene unos y ceros es un tipo especial de vector o matriz denominado lógico y se utiliza mucho en MATLAB como vamos a ver en esta página.
Los operadores lógicos
- & AND (el resultado es verdadero si ambas expresiones son verdaderas)
- | OR (el resultado es verdadero si alguna expresión es verdadera)
- ~ NOT (el resultado invierte la condición de la expresión)
AND y OR trabajan con dos operandos y retornan un valor lógico basadas en las denominadas tablas de verdad. El operador NOT actúa sobre un operando. Estas tablas de verdad son conocidas y usadas en el contexto de la vida diaria, por ejemplo: "si hace sol Y tengo tiempo, iré a la playa", "si NO hace sol, me quedaré en casa", "si llueve O hace viento, iré al cine". Las tablas de verdad de los operadores AND, OR y NOT se muestran en las tablas siguientes
- El operador lógico AND, &
| x | y | Resultado |
|---|---|---|
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
- El operador lógico OR, |
| x | y | Resultado |
|---|---|---|
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
- El operador lógico NOT, ~
| x | Resultado |
|---|---|
| 1 | 0 |
| 0 | 1 |
Los operadores AND y OR combinan expresiones relacionales cuyo resultado viene dado por la última columna de sus tablas de verdad. Por ejemplo:
(a<b) & (b<c)
es verdadero, si ambas son verdaderas. Si alguna o ambas son falsas el resultado es falso. En cambio, la expresión
(a<b)|(b<c)
es verdadera si una de las dos comparaciones lo es. Si ambas, son falsas, el resultado es falso. La expresión " NO a es menor que b"
~(a<b)
es falsa si (a<b) es verdadero y es verdadera, si la comparación es falsa. Por tanto, el operador NOT cambia el estado de verdadero a falso y de falso a verdadero.
MATLAB dispone de funciones que son equivalentes a los operadores lógicos. Estas son:
and(x,y) equivalente a x&y
or(x,y) equivalente a x|y
not(x) equivalente a ~x
Los operadores lógicos en combinación con los relacionales se pueden aplicar también a vectores,
>> a=[1 5 3 7];
>> b=[0 2 8 7];
>> u=(a>b) & (a>4)
u=
0 1 0 0
>> u=(a>b) | (a>4)
u=
1 1 0 1
Acceso a los elementos de un vector
Ya hemos estudiado como se accede a los elementos de un vector o una matriz a través de sus índices, en esta página vamos a ver nuevas formas de acceder dichos elementos cuando cumplen determinadas condiciones.
Para obtener los elementos del vector a que son menores que 10
>> a=[15 6 9 4 11 7 14] a= 15 6 9 4 11 7 14 >> u=a<10 u = 0 1 1 1 0 1 0 >> c=a(u) c = 6 9 4 7
Como vemos el vector u=a<10 contienen unos y ceros como resultado de la comparación de cada uno de los elementos del vector a con 10. Si es menor devuelve 1 si es mayor o igual devuelve 0. Sin embargo, c=a(u) crea un vector formado por aquellos elementos del vector a que se corresponden con 1 en el vector u.
Sea el vector x=[-4,0,5,-3,0,3,7,-1,6];, vamos a contar cuantos elementos del vector x son positivos, negativos o nulos
>> x=[-4,0,5,-3,0,3,7,-1,6] x = -4 0 5 -3 0 3 7 -1 6 >> u=x<0 u = 1 0 0 1 0 0 0 1 0 >> ne=sum(u) ne = 3 >> pos=sum(x>0) pos = 4 >> cero=sum(x==0) cero = 2
Producto de un vector por un vector lógico
Vamos a calcular el producto elemento a elemento del vector a por el vector lógico u, que utilizaremos en los siguientes apartados
>> a=[15,6,9,4,11,7,14]
a = 15 6 9 4 11 7 14
>> u =[0,1,1,1,0,1,0]
u = 0 1 1 1 0 1 0
>> a.*u
ans =
0 6 9 4 0 7 0
Representar la parte positiva de una función
Representar la función f(x) definida del siguiente modo
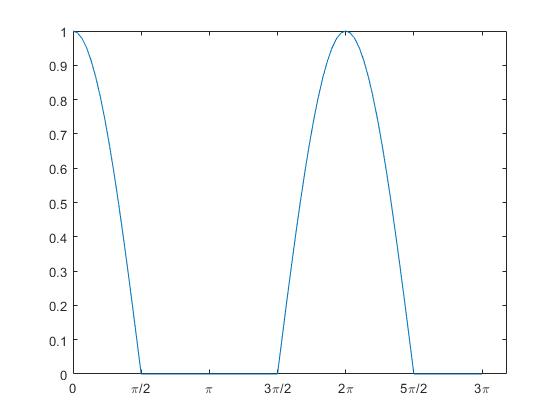
x=0:pi/30:3*pi;
y=cos(x);
y=y.*(y>0);
plot(x,y)
set(gca,'XTick',0:pi/2:3*pi)
set(gca,'XTickLabel',{'0','\pi/2','\pi','3\pi/2','2\pi','5\pi/2','3\pi'})
La expresión (y>0) devuelve un vector cuyos elementos son 1 cuando cos(x) es positivo y 0 en caso contrario. El producto elemento a elemento y.*(y>0) conserva inalterados los valores positivos y los otros los hace cero.
Representar una función escalón
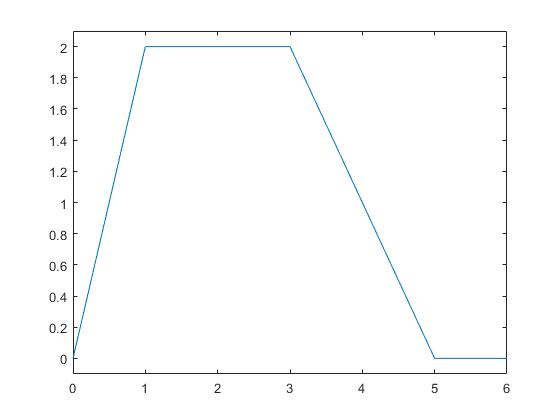
x=0:0.01:6; y=(2*x).*(0<=x & x<1)+2*(1<=x & x<3)+(-x+5).*(3<=x & x<5); plot(x,y) ylim([-0.1 2.1])
Evitando la división entre cero
Supongamos que queremos dibujar la gráfica de la función y=sin(x)/x desde -4π a 4π. Pero cuando x es cero tenemos una división entre cero. Un modo de evitar este problema es sustituir x=0 por x=eps. Si escribimos eps en la ventana de comandos obtenemos un número muy pequeño 2.2204e-016.
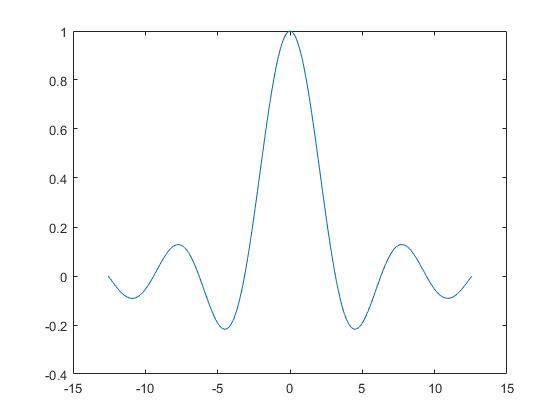
x=-4*pi:pi/30:4*pi; x=x+(x==0)*eps; y=sin(x)./x; plot(x,y)
La expresión (x==0) devuelve un uno cuando x=0, entonces x toma el valor final x=eps que evita la división entre 0.
Evitando el infinito
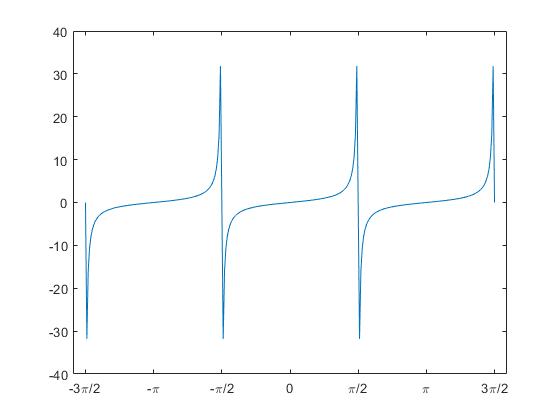
Vamos a dibujar la función y=tan(x) desde -3π/2 a 3π/2. El problema es que tan(x) se aproxima a ±∞cuando x=±π/2, ±3π/2, ...
x=-3*pi/2:pi/100:3*pi/2;
y=tan(x);
y=y.*(abs(y)<100);
plot(x,y)
set(gca,'XTick',-3*pi/2:pi/2:3*pi/2)
set(gca,'XTickLabel',{'-3\pi/2','-\pi','-\pi/2','0','\pi/2','\pi','3\pi/2'})
abs(y)<100 devuelve un vector que es cero solamente cerca de las asíntotas (cuando la tangente es muy grande en valor absoluto), y un uno en los demás casos. Se sugiere poner un símbolo comentario % delante de la tercera línea para anularla, guardar el script y probar el efecto.
Funciones MATLAB
| xor(a,b) | OR exclusivo. Devuelve 1 si un operando es verdadero y el otro es falso. Devuelve 0 si los dos son verdaderos o los dos son falsos. | >> xor(7,0) ans = 1 >> xor(7,-5) ans = 0 |
|---|---|---|
| all(a) | Devuelve 1 si todos los elementos del vector son distintos de cero. Devuelve 0 si uno o más elementos son cero | >>a = [5 3 11 7 8 15]; >> all(a) ans =1 >> b = [3 6 11 4 0 13]; >> all(b) ans = 0 |
| any(a) | Devuelve 1 si hay elementos del vector que son distintos de cero. Si todos los elementos del vector son cero devuelve cero. | >> a = [5 0 14 0 0 13]; >> any(a) ans =1 >> b = [0 0 0 0 0 0 ]; >> any(b) ans = 0 |
| find(a) find(a>d) |
Devuelve los índices de los elementos del vector distintos de cero Si a es un vector, find devuelve los índices de los elementos que son mayores que d (se puede utilizar cualquier otro operador relacional distinto a a>d) |
>> a = [0 7 4 2 8 0 0 3 9]; >> find(a) ans =2 3 4 5 8 9 >> find(a>4) ans=2 5 9 |
Ejemplos
1.- Las temperaturas máximas del 1 al 28 de febrero han sido:
15, 14, 10, 12, 6, 8, 12, 16, 18, 20, 17, 15, 13, 11, 9, 7, 5, 4, 6, 8, 12, 13, 15, 19,
21, 23, 16, 14
Determinar el número de días y las fechas en la que la temperatura máxima del día es mayor o igual a 15 grados centígrados
Como hemos visto, T>=15 es un vector cuyos elementos toman el valor de 1 si se cumple la condición y 0 en caso contrario.
>> T=[15 14 10 12 6 8 12 16 18 20 17 15 13 11 9 7 5 4 6 8 12 13 15
19 21 23 16 14];
>> length(T)
ans = 28
>> dias=sum(T>=15)
dias = 11
>> fechas=find(T>=15) %índices de los elementos del vector T que son >= que 15
fechas =
1 8 9 10 11 12 23 24 25 26 27
>> length(fechas)
ans = 11
En el caso de la función all se puede emplear en sentencias de este tipo: Si todos los elementos del vector a son mayores que uno, hacer alguna tarea. Del mismo modo se puede emplear la función any.
if all(a>1)
hacer algo...
end
2.-En el siguiente vector guarda las edades de varias personas: edad=[45,47,15,23,7,60,35,28,32,10,41]. Determinar
- El número total de personas,
>> edad=[45,47,15,23,7,60,35,28,32,10,41]; >> length(edad) ans = 11
>> adultos=edad>20 adultos = 1 1 0 1 0 1 1 1 1 0 1 >> n_adultos=sum(adultos) n_adultos = 8
>> ninhos=edad<=10 ninhos = 0 0 0 0 1 0 0 0 0 1 0 >> n_ninhos=sum(ninhos) n_ninhos = 2
>> jovenes=edad>10 & edad<=20 jovenes = 0 0 1 0 0 0 0 0 0 0 0 >> n_jovenes=sum(jovenes) n_jovenes = 1 >> n_ninhos+n_adultos+n_jovenes ans = 11
>> any(edad<=10) ans = 1
>> all(edad>20) ans = 0
Creamos un vector de datos de los pesos de las personas: peso=[70,83,45,60,25,55,90,73,65,35,78]
- ¿Cuantos adultos pesan más de 65 kg?
>> edad=[45,47,15,23,7,60,35,28,32,10,41]; >> peso=[70,83,45,60,25,55,90,73,65,35,78]; >> edad>20 ans = 1 1 0 1 0 1 1 1 1 0 1 >> peso>65 ans = 1 1 0 0 0 0 1 1 0 0 1 >> edad>20 & peso>65 ans = 1 1 0 0 0 0 1 1 0 0 1 >> sum(edad>20 & peso>65) ans = 5
>> edad=[45,47,15,23,7,60,35,28,32,10, 41]; >> find(edad>20) ans = 1 2 4 6 7 8 9 11 >> adultos=edad(find(edad>20)) adultos = 45 47 23 60 35 28 32 41 >> length(adultos) ans = 8
>> edad=[45,47,15,23,7,60,35,28,32,10,41]; >> peso=[70,83,45,60,25,55,90,73,65,35,78]; >> indices=find(edad>20) indices = 1 2 4 6 7 8 9 11 >> peso(indices(3)) ans = 60
3.-Dado el vector v=1:16;
>> v v = 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
- Mostrar los números pares mayores que 4
>> v(rem(v,2)==0 & v>4) ans = 6 8 10 12 14 16
>> v=1:16; >> v(rem(v,3)==0)=[] v = 1 2 4 5 7 8 10 11 13 14 16
4.- Una empresa paga los siguientes tipos de salario anual: 12000, 15000, 18000, 24000, 35000, 50000 y 70000. El número de empleados en cada una de las categorías es: 3000, 2500, 1500, 1000, 400, 100 y 25. Calcular:
- El número total de empleados
- El número de empleados de la empresa cuyos salarios son superiores a 32000 e inferiores a dicha cantidad
- El salario medio por empleado en la empresa (media ponderada)
>> salario=[12000,15000,18000,24000,35000,50000,70000]; >> empleados=[3000,2500,1500,1000,400,100,25]; >> n_empleados=sum(empleados) n_empleados = 8525 >> u=salario>32000 u = 0 0 0 0 1 1 1 >> u.*empleados ans = 0 0 0 0 400 100 25 >> n_alto=sum(u.*empleados) n_alto = 525 >> n_bajo=n_empleados-n_alto n_bajo = 8000 >> salario_medio=sum(empleados.*salario)/n_empleados salario_medio = 1.7038e+004
5. El recibo de la electricidad de los residentes en una determinada ciudad se calcula del siguinete modo:
- Si se consumen 500 Kwh o menos el coste es de 2 céntimos por Kwh
- Si se consumen más de 500 Kwh y pero no más de 1000 el coste es 10 euros por los primeros 500 Kwh y 5 céntimos por Kwh para el consumo que exceda los 500 Kwh
- Si se consumen más de 1000 Kwh el coste es 35 euros por los primeros 1000 Kwh y 10 céntimos por Kwh para el consumo que exceda los 1000 Kwh
- La compañía eléctrica incluye un gasto fijo de 5 euros, independiente del consumo.
Las lecturas del contador de electricidad de cinco familias ha sido el siguiente: 200, 500, 700, 1000, 1500 Kwh, respectivamente. Mostrar los resultados del cálculo en dos columnas, una del cosumo y la otra del coste de la electricidad consumida.
consumo=[200,500,700,1000,1500]; coste=5+10*(consumo>500)+25*(consumo>1000); coste=coste+0.02*(consumo<=500).*consumo; coste=coste+0.05*(consumo>500 & consumo<=1000).*(consumo-500); coste=coste+0.1*(consumo>1000).*(consumo-1000); disp([consumo',coste'])
200 9
500 15
700 25
1000 40
1500 90

