Gráficos bidimensionales

Gráficos bidimensionales (II)

fill

El comando fill rellena áreas del color especificado

En este ejempo, dibujamos una elipse y un polígono de 10 lados inscrito en la elipse. Calculamos el área del polígono con la función polyarea

%elipse
a=2; b=5; 
t=linspace(0, 2*pi, 200);
x=a*cos(t);
y=b*sin(t);
hold on
plot(x,y,'b')
%polígono
t=linspace(0, 2*pi, 11);
x=a*cos(t);
y=b*sin(t);
fill(x,y,'y')
plot(x,y,'ro','markersize',4,'markeredgecolor','r','markerfacecolor','r')
hold off
title('área de un polígono')
disp(['Area = ' num2str(polyarea(x, y))])

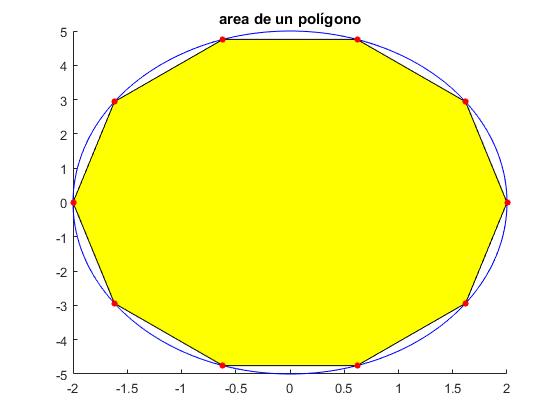
Area = 29.3893

El área de la elipse es πab=π·2·5=31.4159

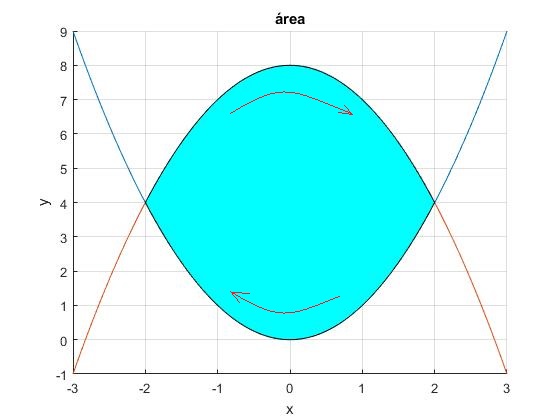
Dibujamos dos funciones y=-x² e y=-x²+8, que se cortan en los puntos ±2 y rellenamos el área comprendida entre las dos funciones. Para encerrar el área (véase la figura más abajo) especificamos la primera función y=-x² entre -2 y +2 y la segunda y=-x²+8, entre +2 y -2. Para ello, invertimos el sentido de los vectores x e y mediante la función fliplr. Esta función hace que el último elemento del vector x pasa a ser el primero.

hold on
fplot('x^2',[-3,3])
fplot('-x^2+8',[-3,3])
x=-2:0.05:2;
fill([x,fliplr(x)],[x.^2,fliplr(-x.^2+8)],'c')
hold off
grid on
xlabel('x')
ylabel('y')
title('área')

stem

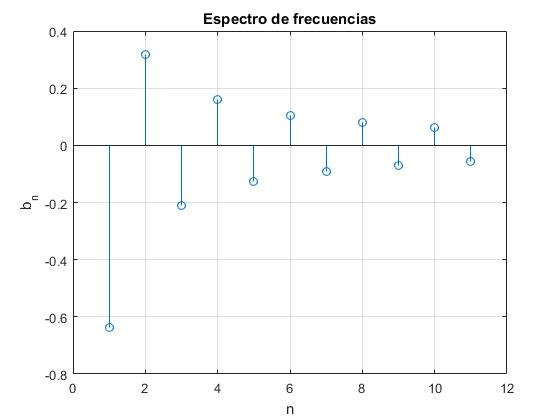
Se ha analizado una señal periódica y los coeficientes b_n (seno) del desarrollo en serie de Fourier tienen la expresión

$b_{n} = 2 \frac{{(- 1)}^{n}}{n π}$

Representamos mediante stem la contribución de cada uno de los armónicos (n=1,2,3...) al desarrollo en serie de Fourier de la función.

n=1:11;
bn=(-1).^n*2./(n*pi);
stem(bn)
title('Espectro de frecuencias')
xlabel('n')
ylabel('b_n')
xlim([0 12])

bar

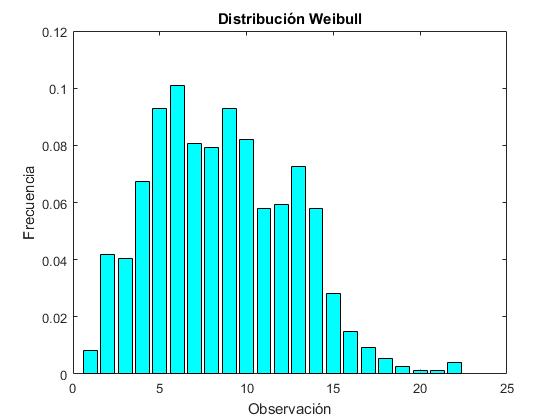
Se han realizado las siguientes observaciones de la velocidad del viento en una estación meteorológica. Medimos el número de horas en las que la velocidad del viento tenía un valor medio comprendido entre 0 y 1 m/s, entre 1 y 2, ... entre 22 y 23.

Velocidad	0.5	1.5	2.5	3.5	4.5	5.5	6.5	7.5	8.5	9.5	10.5	11.5	12.5	13.5	14.5	15.5	16.5	17.5
Horas	6	31	30	50	69	75	60	59	69	61	43	44	54	43	21	11	7	4
Velocidad	18.5	19.5	20.5	21.5
Horas	2	1	1	3

Vamos a representar las frecuencias mediante un diagrama de barras.

x=0.5:21.5;
horas=[6,31,30,50,69,75,60,59,69,61,43,44,54,43,21,11,7,4,2,1,1,3];

frec=horas/sum(horas);
bar(frec,'c');
title('Distribución Weibull')
xlabel('Observación')
ylabel('Frecuencia')

Histogramas, hist

El intervalo (a, b) que abarca todos los datos, se divide en subintervalos. El histograma es un diagrama de barras verticales en el que la anchura de cada barra se corresponde con el tamaño del subintervalo y la altura con el número de datos en dicho subintervalo.

Por defecto, MATLAB divide el intervalo (a,b) en 10 subintervalos de la misma anchura.

y=[53,50,93,89,91,80,59,69,56,64,69,63,74,82,84,91,
63,66,48,56,73,73,66,64,74,63,69,58,73,73]; 
hist(y)
xlabel('T')
ylabel('n')
title('Temperaturas')

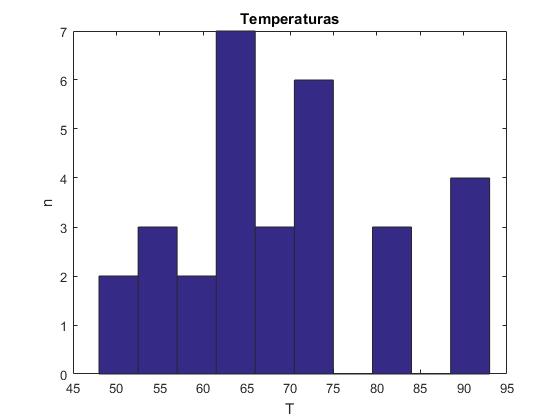
>> min(y)
ans =    48
>> max(y)
ans =    93

El valor mínimo del vector y es 48 y el valor máximo es 93, la diferencia es de 45, por lo que el tamaño de cada subintervalo es 4.5. El primer subintervalo va de 48 a 52.5 está centrado en 50.25 y contiene dos datos. El segundo subintervalo va de 52.5 a 57, está centrado en 54.75 y contiene tres datos. Dos subintervalos: (75 a 79.5) y (84 a 88.5) no contienen datos

>> [N,X]=hist(y)
N =     2     3     2     7     3     6     0     3     0     4
X =   50.2500   54.7500   59.2500   63.7500   68.2500   72.7500   77.2500   
81.7500   86.2500   90.7500

La función hist, devuelve el número de datos N en cada subintervalo y el centro X de cada uno de ellos

La función randn devuelve números aleatorios comprendidos entre 0 y 1 tomados de una distribución normal, cuyo valor medio es x0 y cuya desviación estándar es sigma. Se compara el diagrama de barras con la representación gráfica de la función de distribución

x0=1; % valor medio
sigma=0.5; % desviación estándar
xp=x0+sigma*randn(1,10000); %vector de N números aleatorios
hold on
[n,xs]=hist(xp, 25); 
bar(xs, n); 
xlabel('Valores')
ylabel('Número de datos')
f=@(x) max(n)*exp( -(x-x0).^2/(2*sigma^2));
fplot(f,[-0.5,2.5],'r')
hold off

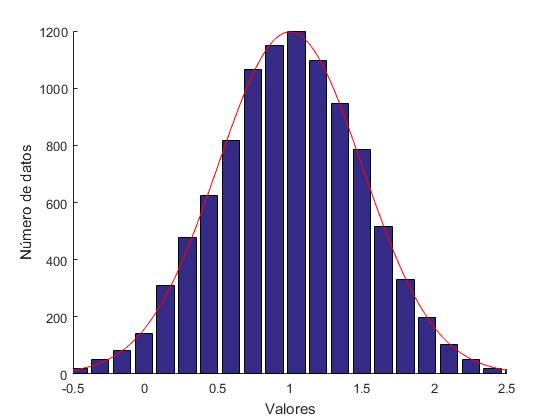
Es posible cambiar el valor por defecto. Se le puede suministrar a la función hist un vector x, cuyos valores son los centros de cada uno de los subintervalos tal como vemos en la figura, los subintervalos pueden tener distinta anchura.

Se miden las temperaturas a lo largo de un periodo de 30 días en una ciudad. La temperatura mínima es a=5 grados y la máxima b=35 grados. Dividimos el intervalo en tres subintervalos centrados en 10, 20 y 30 grados que nos indican el número de días con temperatura fría, templada y cálida.

Las temperaturas se generan de forma aleatoria mediante la función rand

a=5; %temperatura mínima
b=35; %temperatura máxima
T=round(a+(b-a)*rand(30,1)); %30 temperaturas al azar
x=a+5:10:b;
hist(T,x)
hg=findobj(gca,'Type','patch'); %color
set(hg,'FaceColor','c','EdgeColor','k')
xlabel('Temperatura')
ylabel('n. de días')
title('Temperatura en una ciudad')

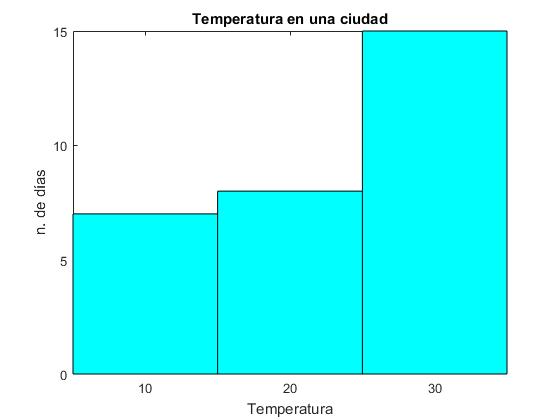
semilog, loglog

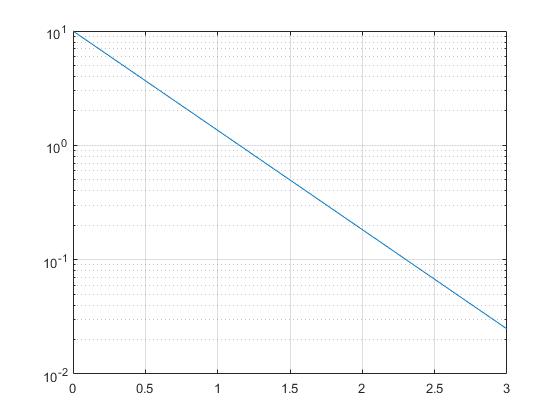
Son útiles cuando hacemos representaciones gráficas de funciones exponenciales o potenciales. Representamos la función 10·exp(-2·x) utilizando el comando semilogy.

x=linspace(0,3);
y=10*exp(-2*x);
semilogy(x,y)
grid on

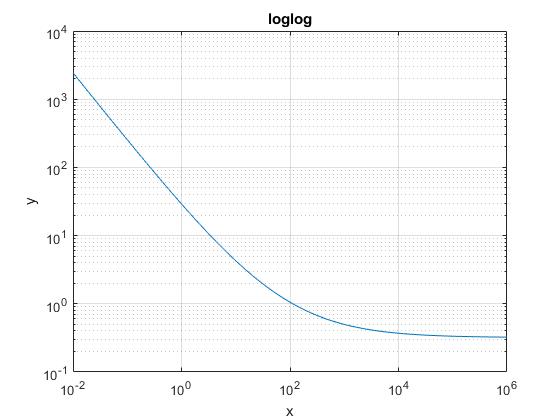
Representamos la siguiente función en un diagrama doblemente logarítmico

$y = {({(\frac{a}{x})}^{c} + b^{c})}^{1 / c}$

con a=24, b=0.32 y c=0.52

a=24;
b=0.32;
c=0.52;
f=@(x) ((a./x).^c+b^c).^(1/c);

x=logspace(-2,6,100);
loglog(x,f(x))
grid on
xlabel('x')
ylabel('y')
title('loglog')

polar

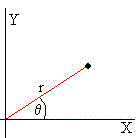
Las coordenadas polares especifican un punto en términos de la distancia (radio) al origen r y el ángulo θ que forma con el eje X.

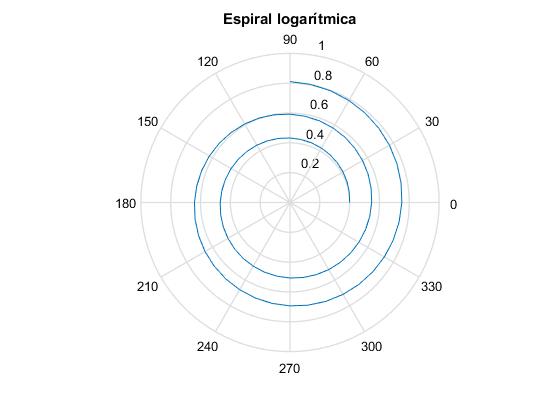
La espiral logarítmica es una de las curvas notables junto a la catenaria, la cicloide, etc. La ecuación de la espiral logarítmica en coordenadas polares es

r=r₀·exp(b·θ)

Donde r₀ es el radio inicial, b es un parámetro, y θ es el ángulo en radianes.

r0=0.4; 
b=0.05; 
ang=0:pi/18:9*pi/2;
r=r0*exp(b*ang);
polar(ang,r,'r')
title('Espiral logarítmica')

Utilizando la función pol2cart, que convierte coordendas polares a coordenadas rectangulares, obtenemos un resultado similar mediante el comando plot en vez del comando polar

r0=0.4;
b=0.05;
ang=0:pi/18:9*pi/2;
r=r0*exp(b*ang);
[x,y]=pol2cart(ang,r);
plot(x,y,'r')
axis equal
title('Espiral logarítmica')
grid on

En Internet se pueden encontrar las ecuaciones de curvas polares como las cardiodes

r=b+a·cosθ
r=b+a·sinθ

en los siguientes casos: b<a, a<b<2a, 2a≤b. El primero es el más interesante.

Otra curva es la denominada pétalos de una rosa

r=a·cos(nθ)

donde n es el número entero: 2, 3, 4, 6...

La lemniscata de Bernoulli

r²=2a²cos(2θ)

Manejadores de los gráficos

Siempre que MATLAB crea un gráfico, crea un manejador (handle) para este gráfico. Vamos a ver mediante ejemplos como se pueden cambiar las propiedades del gráfico mediante manejadores.

La función plot devuelve el manejador del gráfico actual, mediante la función set se pueden cambiar sus propiedades.

>> x=0:pi/30:2*pi;
>> hg=plot(x,sin(x));
>> set(hg,'color','r','linewidth',3)

El gráfico que inicialmente tenía color azul (por defecto) cambia a color rojo. La anchura de línea cambia a tres.

gca es una referencia (handle) que identifica los ejes de la gráfica y a través de este manejador podemos cambiar el aspecto de los ejes. xTick es la propiedad (división del eje horizontal) y a continuación, se pone el nuevo valor de dicha propiedad 0:pi/2:2*pi.

x = 0:.02:2*pi;
y = cos(x);
plot(x,y)
set(gca,'XTick',0:pi/2:2*pi)
set(gca,'XTickLabel',{'0','\pi/2','\pi','3\pi/2','2\pi'})
set(gca,'YTick',-1:0.25:1)

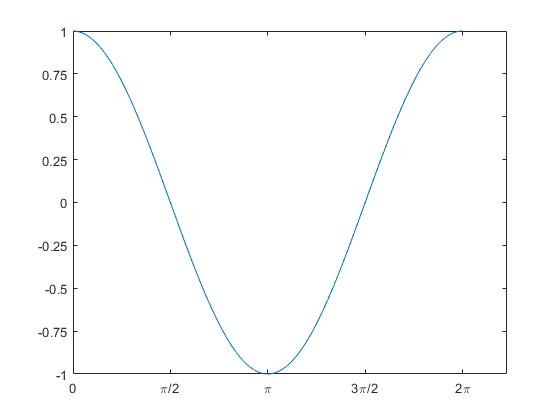
De esta forma, podemos cambiar las divisiones por defecto de los ejes X e Y.

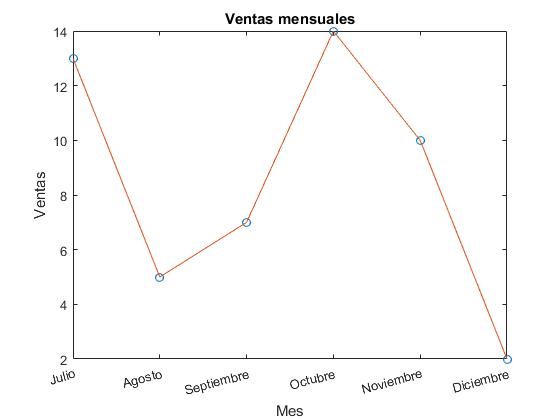
En este ejemplo, las divisiones XTick del eje X tienen un nombre XTickLabel muy largo y es necesario girarlas XTickLabelRotation, para que sean legibles

x=1:6;
y=[13,5,7,14,10,2];
plot(x,y,'o',x,y)
set(gca,'XTick',x);
set(gca,'XTickLabel',{'Julio','Agosto','Septiembre','Octubre',
'Noviembre','Diciembre'}, 'XTickLabelRotation',15)
xlabel('Mes')
ylabel('Ventas')
title('Ventas mensuales')

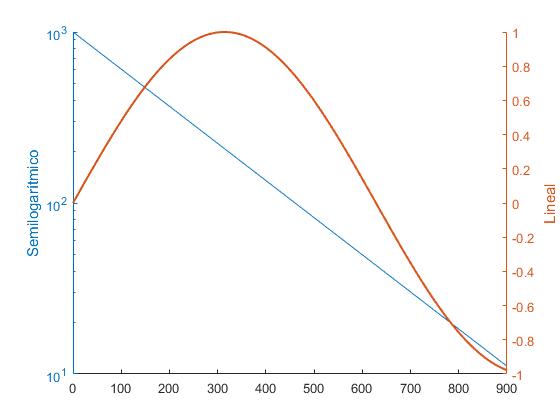
Combinando ejes lineales y logarítmicos

Podemos utilizar plotyy para comparar dos gráficas que tinene distintas escalas

a=1000;b=0.005;
t=0:900;
y1=a*exp(-b*t);
y2=sin(b*t);
[ha,h1,h2] = plotyy(t,y1,t,y2,'semilogy','plot');
axes(ha(1)) %eje de la izquierda
ylabel('Semilogarítmico')
axes(ha(2)) %eje de la derecha
ylabel('Lineal')
set(h2,'linewidth',1.5) %gráfica 2

Dibujamos la primera función y1 a escala semilogarítmica y la segunda función y2 a escala normal. El comando plotyy devuelve una referencia (handle) a los ejes en ha, una referencia al primer gráfico en h1 y una referencia al segundo en h2. Como hay dos ejes ha es un vector de dos elementos, ha(1) es una referencia al eje izquierdo y ha(2) al eje derecho. Modificamos la anchura de línea del segundo gráfico h2 con la función set.

Edición en la ventana de los gráficos

Escribimos en la ventana de comandos

>> x=0:pi/40:2*pi;
>> plot(x,cos(x))

En la ventana de los gráficos (Figure Window) podemos cambiar las propiedades de un gráfico. Seleccionamos Tools->Edit Plot

Se selecciona el gráfico con el cursor, aparecen cuadrados de color negro (handles), se pulsa el botón derecho del ratón estando el gráfico seleccionado, aparece el menú de la figura, que nos permite cambiar varias propiedades del gráfico: color, anchura y estilo de línea, marcador, etc.

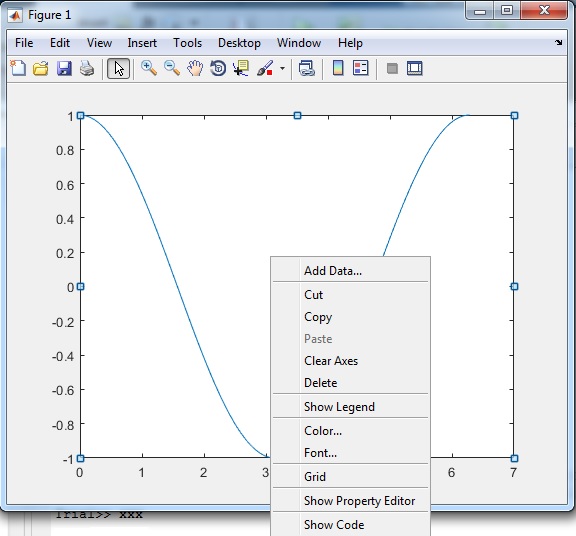
Se puede utilizar el menú Insert para establecer las etiquetas de los ejes (xlabel, ylabel), el título (title), legend, etc. Dibujar líneas, elipses, rectángulos, insertar textos, etc.

Seleccionando Show Property Editor, o bien, en el menú View->Property Editor o en el menú Edit->(Figure Properties, Axes properties, Current Object Properties, Colormap) aparece una ventana que nos permite cambiar las propiedades del gráfico de forma interactiva. Pulsamos en el botón More properties... aparece una tabla (Inspector) de propiedades del objeto seleccionado que podemos modificar.

La edición interactiva en la ventana de los gráficos, nos permite prepararlos para presentaciones, pero escasamente se utilizará en los cálculos, por lo que queda al lector la tarea de explorar sus numerosas opciones, consultando el extenso documento MATLAB Graphics

Ejemplos en el curso de Física

plot

La mayor parte de las porciones de código MATLAB, terminan con una representación gráfica, por lo que la lista de páginas en las que se utiliza el comando plot es demasiado numerosa para mencionarlas en este apartado.

fill

stem

bar

Histogramas, hist

semilog, loglog

polar

Manejadores de los gráficos

Combinando ejes lineales y logarítmicos

Edición en la ventana de los gráficos

Ejemplos en el curso de Física

plot

fplot

polar

pie

stem

bar, barh

quiver

fill

subplot