Funciones

Estamos acostumbrados a trabajar con funciones del tipo y=f(x) donde f(x) es una expresión matemática en términos de la variable x. Se calcula un valor de y (salida) cuando se proporciona un valor de x (entrada) en la expresión. MATLAB define muchas funciones como sin(x), sqrt(x), etc.

Podemos definir nuestras propias funciones guardarlas en un fichero y usarlas de un modo semejante a las funciones predefinidas. En muchos casos las funciones son los componentes básicos dentro de un programa de ordenador. Habitualmente, un programa se subdivide en tareas y cada una de ellas es llevada a cabo por una función, a esta forma de resolver los problemas se denomina programación estructurada.

La principal ventaja de las funciones es la posibilidad de reutilizar el código en otros programas distintos al cual fueron definidas.

El aspecto más importante de esta página, son las funciones anónimas, que se utilizarán con mucha frecuencia en la programación con MATLAB

La entrada y la salida puede ser una o varias variables, cada una de ellas puede ser un escalar, un vector o una matriz de cualquier tamaño.

funcion

Definición de una función

Las funciones se crean del mismo modo que un script seleccionado en el menú New/Function y se guardan en un fichero que tiene el mismo nombre que la función y extensión .m

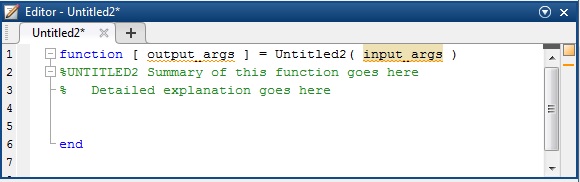
plantilla

La primera línea en el editor es la definición de la función que comienza con la palabra clave function

function variables_salida=nombre_funcion(variables_entrada)
    sentencias
end

nombre_funcion, es el nombre significativo que se le asigna a la función y coincide con el nombre del fichero de extensión .m en el que se guarda el código de dicha función. Las reglas para nombrar un función son las mismas que para las variables, los nombres no deben de incluir espacios, ni se pueden utilizar plabras reservadas por MATLAB.
variables_entrada, es el conjunto de parámetros que se le pasa a la función. Los nombres de las variables van entre paréntesis y separadas por coma.
variabales_salida, es el valor o conjunto de valores de las variables devueltos por la función. Las variables de salida van después de la palabra reservada function entre corchetes cuadrados y separados por comas si hay varios.
sentencias, líneas de código que tomando los valores de los parámetros de entrada calculan mediante expresiones los valores que devuelve la función.
end, marca el final de la función es opcional (salvo en las funciones anidadas) pero es conveniente acostumbrarse a ponerlo al finalizar la función.

Opcionalmente, en la segunda línea se pone un comentario, en el que se explica la tarea que realiza la función. A continuación, una explicación detallada sobre las variables de entrada y de salida

Cuando una función no devuelve ningún valor, se define

function nombre_funcion(variables_entrada)

Cuando una funcion no precisa de variables de entrada se define

function variables_salida=nombre_funcion

Cuando una función devuelve una solo resultado y se puede escribir, de dos maneras

function [y]=nombre_funcion(a,b,c) function y=nombre_funcion(a,b,c)

En general, definiremos una función del siguiente modo:

function [y1,y2]=nombre_funcion(a,b,c)

con tres argumentos a, b y c variables de entrada y que devuelve dos resultados en las variables y1 e y2.

Una función se llama del mismo modo que las funciones predefinidas. Las funciones se pueden llamar desde la ventana de comandos, desde un fichero script o desde otra función.

Todas las variables en una función son locales a dicha función, incluyendo las de entrada y las de salida.

Vamos a ver unos cuantos ejemplos en esta página de funciones.

Ejemplos

Suma de dos números

Empezaremos por una función suma que realiza la siguiente tarea, suma de dos números x e y y devuelve la suma z=x+y

Definición de la función

function [z] = suma (x,y)
%Esta función suma dos números x e y
%y devuelve el resultado de la suma en z

    z=x+y; %efectúa la suma
end

A la función suma se le pasan dos datos en las variables x e y, y devuelve el resultado en la variable z.

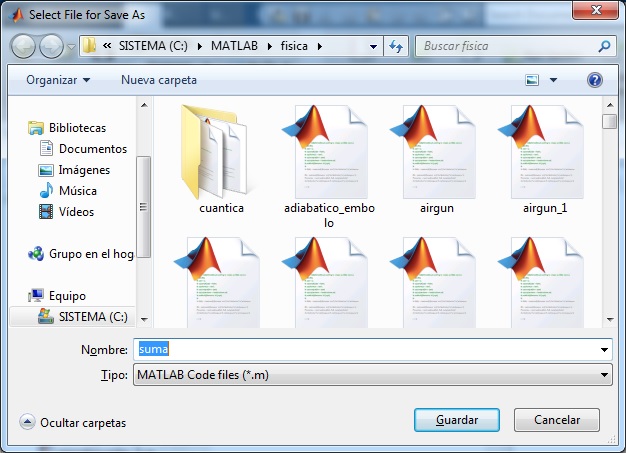
La función se guarda en un fichero

El fichero que guarda la función tiene el mismo nombre que la función, tal como vemos al seleccionar en el Editor File/Save as...

Llamada a la función

La llamada a la función se puede hacer desde la ventana de comandos

>> suma(2,3)
ans =     5

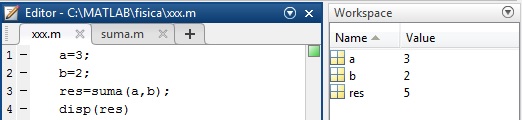
Se puede hacer desde un script

a=3;
b=2;
res=suma(a,b);
disp(res)

En la llamada a la función suma su parámetro x adquiere el valor del primer argumento a, el segundo parámetro y toma el valor del argumento b, se efectúa la suma en el cuerpo de la función, se guarda el resultado en la variable z que devuelve la función. El valor que guarda z se copia en la variable res. Las variables x, y y z son locales a la función y por tanto, no aparecen en la ventana Workspace, no se puede acceder a ellas desde la ventana de comandos.

>> suma(2,3)
ans =     5
>> x
Undefined function or variable 'x'.
>> z
Undefined function or variable 'z'.

Como hemos visto hay que pasar los valores que guardan las variables a y b a la función suma por que una función no tiene acceso a las variables declaradas en un script o en la ventana de comandos.

Sistema de ayuda

En la ventana de comandos escribimos

>> help suma
 Esta función suma dos números x e y
  y devuelve el resultado de la suma en z

aparecen los comentarios que hemos puesto al principio de la función, pero no aparecen el comentario "efectúa la suma", que hemos puesto en la tercera línea.

Movimiento de caída de los cuerpos

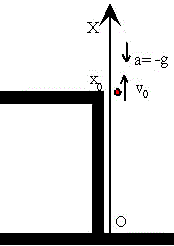
Las ecuaciones que describen el movimiento de caída de los cuerpos son:

$\begin{array}{l} v = v_{0} + g \cdot t \\ x = x_{0} + v_{0} t + \frac{1}{2} g t^{2} \end{array}$

Donde v₀ y x₀ es la velocidad inicial y la posición inicial, respectivamente. Vamos a crear una función denominada caida_libre que admita como parámetros el tiempo t y devuelva la posición x y velocidad v de un móvil que se lanza desde 200 m de altura con velocidad de 40 m/s. La aceleración constante de la gravedad g=-10 m/s²

v=40-10·t
x=200+40·t-5·t²

Seleccionamos New/Function para abrir el editor de funciones.

Definimos la función:

La palabra clave function
Las variables de salida entre corchetes cuadrados [x,v]
El operador asignación =
El nombre de la función, caida_libre
Entre paréntesis la variable de entrada (t)

Escribimos el cuerpo de la función con dos sentencias que calculan la velocidad v y la posición x cuando se proporciona el dato del tiempo t
Finalizamos con end.
Seleccionamos Save para guardar la función en el fichero caida_libre.m con el mismo nombre que la función.

function [x,v] = caida_libre(t)
    v=40-10*t;    
    x=200+40*t-5*t^2;
end

En la ventana de comandos se llama a esta función caida_libre, pasándole un tiempo t=2 s, del siguiente modo

>> [pos,vel]=caida_libre(2)
pos =    240
vel =  20

Que calcula y muestra, la velocidad v=20 m/s y la posición x=240 m en el instante t=2 s

En la llamada a la función caida_libre el parámetro t adquiere el valor de 2, en las dos sentencias se calcula la velocidad y posición y se guardan en las variables locales v y x. La función devuelve estos dos valores que se copian en las variables vel y pos de la ventana de comandos. En la ventana de comandos no tenemos acceso a las variables t, v y x por ser locales a la función caida_libre y desaparecen cuando termina de ejecutarse, pero si tenemos acceso a las variables vel y pos que guardan los resultados del cálculo realizado en el cuerpo de la función.

Si intentamos acceder a la variable x o t obtendremos un mensaje de error

>> x,t
??? Undefined function or variable 'x'.

Si queremos que la función caida_libre calcule la posición y velocidad del móvil para una secuencia (vector) de tiempos t, tendremos que modificar la definición de dicha función

function [x,v] = caida_libre(t)
    v=40-10*t;
    x=200+40*t-5*t.^2;
end

En la ventana de comandos se llama a esta función caida_libre, pasándole los tiempos t=[0,2,4,6,8,10] o bien, t=0:2:10 , del siguiente modo

>> t=0:2:10;
>> [pos,vel]=caida_libre(t)
pos =   200   260   280   260   200   100
vel =    40    20     0   -20   -40   -60

Media y desviación estándar de un conjunto de datos

La definición de media y desviación estándar es la siguiente

$< x > = \frac{\sum_{1}^{n} x_{i}}{n} σ = \sqrt{\frac{\sum_{1}^{n} {(x_{i} - x)}^{2}}{n - 1}}$

Creamos una función denominada estadistica a la que se le pasa un vector x de datos y devuelve la media med y la desviación, des, y la guardamos en un fichero con el mismo nombre que la función

function [med,des]=estadistica(x)
    n=length(x);
    med=sum(x)/n;
    des=sqrt(sum((x-med).^2/(n-1)));
end

La función sum calcula la suma de los elementos de un vector x
La función length, calcula el número de elementos del vector x.

Calcular la media y la desviación estándar de la altura de los 10 alumnos de una clase:
1.65, 1.82, 1.72, 1.75, 1.73, 1.85, 1.90, 1.74, 1.76, 1.77.

Escribimos el nombre de la función estadistica en la ventana de comandos y le pasamos el vector de datos

>> [media, desviacion]=
estadistica([1.65 1.82  1.72 1.75 1.73 1.85 1.90 1.74 1.76 1.77])
media = 1.7690
desviacion = 0.0713

MATLAB dispone de dos funciones que calculan la media mean y la desviación estándar, std.

>> x=[1.65 1.82 1.72 1.75 1.73 1.85 1.90 1.74 1.76 1.77];
>> mean(x)
ans =    1.7690
>> std(x)
ans =    0.0713

Funciones anónimas

Las funciones anónimas nos permiten definir una función simple sin necesidad de crearla y guardarla en un fichero .m. Se pueden definir en la ventana de comandos, en un fichero script o dentro de otra función, con la siguiente sintaxis:

variable=@(parámetros) expresion

expresion consiste en una única y válida expresión, puede tener una o más variables de entrada que se especifican en la lista de argumentos separadas por comas. Puede incluir variables que se han definido previamente

Las funciones se pueden asignar a variables y estas variables se pueden pasar a otras funciones como se pasan escalares o vectores. Más adelante veremos cómo se llama a una función dentro de otra función que se le pasa en uno de sus parámetros.

Comparamos la definición de una función func que se guarda en un fichero func.m y su equivalente anónima

function y=func(x)
    y=cos(x)-x;
end

Llamada a la función

>> z=func(0.5)
z = 0.3776

Su equivalente anónima se escribe en la ventana de comandos sin necesidad de guardarla en un fichero y se llama del mismo modo que cualquier otra función

>> f=@(x) cos(x)-x;
>> z=f(0.5)
z = 0.3776

f guarda un valor asociado a una función que denominaremos manejador ( function handle)

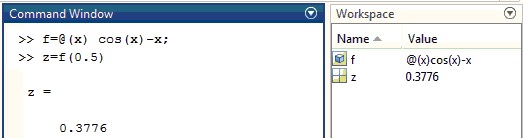
En la ventana Workspace, vemos que aparece una variable f de distinto tipo que guarda la referencia a la función anónima.

Sea una función anónima f que incluye una variable a cuyo valor definimos previamente

>> a=4;
>> f=@(x) a*x;
>> f(3)
ans =    12

Si cambiamos el valor de la variable a, el cambio no tiene efecto en la función f como vemos en el siguiente código

>> a=5;
>> f(3)
ans =    12

Teorema del coseno

Calculamos el lado c del triángulo si conocemos los lados a y b y el ángulo comprendido γ, mediante el teorema del coseno

$c = \sqrt{a^{2} + b^{2} - 2 a b \cos γ}$

>> c=@(a,b,gamma) sqrt(a^2+b^2-2*a*b*cosd(gamma));
>> lado=c(3,4,30)
lado =    2.0531

Nota: MATLAB captura el valor de las variables cuando se define la función anónima. La función anónima f(x) se define con un valor de a=2

>> a=2;
>> f=@(x) cos(a*x);
>> f(0.5)
ans =    0.5403

Ahora cambiamos el valor de la variable a=3, pero la función anónima f(x) no se modifica

>> a=3;
>> f(0.5)
ans =    0.5403

Para que la función f(x) utilice el nuevo valor de a hay que volverla a definir

>> a=3;
>> f=@(x) cos(a*x);
>> f(0.5)
ans =    0.0707

Llamada a una función desde otra función

Existen mucha situaciones en las que una función f1 utiliza otra función f2. Por ejemplo, MATLAB tiene una función fzero que se utiliza para calcular las raíces de una ecuación f(x)=0. La función f se le pasa a fzero cuando se llama para encontrar las raíces de f(x). Hay varias formas de pasar una función f a otra función para su uso.

Ya hemos visto el significado de manejador para una función anónima, un valor que guarda una variable f o c y que está asociado a una función.

Si definimos una función de forma explícita en un fichero por ejemplo, la función func, obtenemos el manejador anteponiendo el carácter @ al nombre de la función

La derivada de una función

Vamos ahora, a ver como se le pasa una función a otra función en uno de sus parámetros.

La derivada primera dy/dx, de una función y=f(x) en un punto x₀, se puede calcular aproximadamente mediante la fórmula

$\frac{d y}{d x} = \frac{f (x_{0} - 2 h) - 8 f (x_{0} - h) + 8 f (x_{0} + h) - f (x_{0} + 2 h)}{12 h}$

donde h un un número pequeño en comparación con x₀. Escribir una función denominada derivada, cuyos parámetros sean la función f, y la abscisa x₀ y devuelva el valor de la derivada de la función f(x) en x₀. Tomar h=10^-5.

function yp= derivada(f,x0)
    h=1e-5;
    yp=(f(x0-2*h)-8*f(x0-h)+8*f(x0+h)-f(x0+2*h))/(12*h);
end

En la ventana de comandos, definimos la función y=x³-6x²+3 (anónima) que queremos derivar y llamamos a la función derivada.

>> f1=@(x) x^3-6*x^2+3;
>> derivada(f1,2)
ans =  -12.0000

Calculamos también la derivada segunda de una función en un punto del siguiente modo

>> f2=@(x) derivada(f1,x);
>> derivada(f2,2)
ans =  9.8686e-007

Comparamos con el valor exacto

$\begin{array}{l} y = x^{3} - 6 x^{2} + 3 \\ \frac{d y}{d x} = 3 x^{2} - 12 x \\ \frac{d^{2} y}{d x^{2}} = 6 x - 12 \end{array}$

Para x₀=2, dy/dx=-12, d²y/dx²=0

Funciones definidas en el mismo fichero

Un fichero función puede contener más de una función. Las funciones se definen una a continuación de la otra. La primera función es la primaria y tiene el mismo nombre que el fichero, las otras funciones son secundarias y se denominan subfunciones y pueden estar en cualquier orden dentro del fichero. Solamente se puede llamar a la función primaria en la ventana de comandos o por otras funciones. Cada función tiene sus propias variables que son locales a la función, no se puede acceder a las variables de una subfunción desde la función primaria o desde otra subfunción. No se puede acceder a las variables de la función primaria desde una subfunción.

Las subfunciones permiten organizar tareas grandes en otras más pequeñas.

Más adelante veremos la utilidad de estas funciones cuando los programas sean más largos y complejos, de momento vamos a ver un ejemplo que nos permita vislumbrar como se definen y llaman las subfunciones.

Ecuación de segundo grado
ax²+bx+c=0
Las raíces son x₁ y x₂ y tienen las siguientes propiedades:

$\begin{array}{l} x_{1} = \frac{- b + \sqrt{b^{2} - 4 a c}}{2 a} x_{2} = \frac{- b - \sqrt{b^{2} - 4 a c}}{2 a} \\ x_{1} + x_{2} = \frac{- b}{a} x_{1} \cdot x_{2} = \frac{c}{a} \end{array}$

Vamos a crear una función que nos permita comprobar las propiedades de las raíces de una ecuación de segundo grado, y dos subfunciones, la primera calcula la raíz x₁ y la segunda la raíz x₂.

En el editor de funciones creamos la función comprobar_raices, a la que se le pasa los coeficientes a, b y c de la ecuación de segundo grado y devuelve los cocientes -b/a y c/a de la suma y producto de las dos raíces x₁ y x₂. Guardamos el código de la función primaria comprobar_raices y de las subfunciones calcula_raiz1 y calcula_raiz2 en el fichero comprobar_raices.m

function [r1,r2]=comprobar_raices(a,b,c)
    x1=calcula_raiz1(a,b,c);
    x2=calcula_raiz2(a,b,c);
        r1=x1+x2;
        r2=x1*x2;
end
            
function raiz=calcula_raiz1(a,b,c)
    raiz=(-b+sqrt(b*b-4*a*c))/(2*a);
end 

function raiz = calcula_raiz2(a,b,c)
    raiz=(-b-sqrt(b*b-4*a*c))/(2*a); 
end

Para comprobar las raíces de la ecuación de segundo grado x²-x-6=0, llamamos a la función comprobar_raices y le pasamos los coeficientes 1,-1,-6 y nos devolverá -b/a=1 y c/a=-6

>> [b_a,c_a]=comprobar_raices(1,-1,-6)
b_a = 1
c_a = -6

Funciones anidadas

Una función anidada es una función definida dentro de otra función. Las función primaria y las anidadas deben obligatoriamente terminar con end

Las funciones anidadas tienen acceso a las variables de la función primaria y la función primaria tiene acceso a las variables definidas por la función anidada.

Una función anidada puede contener otra y así sucesivamente, pero este proceso puede llevar a confusión. Existen reglas para llamar a una función anidada dentro de otra pero no tiene por el momento interés para el lector.

En el editor de funciones creamos la función comprobar_raices1, a la que se le pasa los coeficientes a, b y c de la ecuación de segundo grado y devuelve los cocientes -b/a y c/a de la suma y producto de las dos raíces x₁ y x₂. Guardamos el código de la función primaria comprobar_raices1 y de las subfunciones calcula_raiz1 y calcula_raiz2 en el fichero comprobar_raices1.m

function [r1,r2]=comprobar_raices1(a,b,c)
    dis=sqrt(b*b-4*a*c);
    calcula_raiz1;    
    calcula_raiz2;
    r1=x1+x2;    
    r2=x1*x2;    
    function calcula_raiz1        
        x1=(-b+dis)/(2*a);    
    end     
    function calcula_raiz2        
        x1=(-b-dis)/(2*a);     
    end 
end

Vemos que las funciones anidadas calcula_raiz1 y calcula_raiz2 tienen acceso a los parámetros a, b y c de la función primaria, que son variables locales a la función comprobar_raices y también, a la variable local dis, que guarda el discriminante de la ecuación de segundo grado. Por otra parte, la función primaria tiene acceso a las variables x1 y x2 declaradas en cada una de las funciones anidadas.

Estas funciones anidadas no precisan de variables de entrada y no devuelven nada.

Para comprobar las raíces de la ecuación de segundo grado x²-x-6=0, llamamos a la función comprobar_raices1 y le pasamos los coeficientes 1,-1,-6 y nos devolverá -b/a=1 y c/a=-6

>> [b_a,c_a]=comprobar_raices(1,-1,-6)
b_a = 1
c_a = -6

Como ejercicio se porpone al lector crear la función estadistica_1, que devuelva la media y la desviación estándar, cuando se le pasa un vector de datos. El valor medio se calculará mediante la función anidada media y la desviación estándar mediante la función anidada desviacion.

En primer lugar, creamos la función estadistica_1, y dos funciones auxiliares: la función media y la función desviacion en el mismo fichero estadistica_1.m

function [med,des]=estadistica_1(datos)
    n=length(datos);
    med=media(datos,n);
    des=desviacion(datos,med,n);
end
%calcula la media del vector de datos
function res=media(x,num)
    res=sum(x)/num;    
end
%calcula la desviación estándar
function res=desviacion(x,m,num)
    xd=x-m;    
    xd_suma=sum(xd.^2);
    res=sqrt(xd_suma)/(num-1);
end

Ahora trasladamos las funciones media y desviacion al interior de la función estadistica _1.

function [med,des]=estadistica_1(x)
    n=length(x);
    media;
    desviacion;
 %calcula la media del vector de datos
  function media
        med=sum(x)/n;    
    end  
%calcula la desviación estándar
    function desviacion
        xd=x-med;    
        xd_suma=sum(xd.^2);
        des=sqrt(xd_suma)/(n-1);
    end
end

En la ventana de comandos probamos las dos versiones de la función estadistica_1.

>> [med,des]= estadistica_1([1.65 1.82 1.72 1.75 1.73 1.85 1.90 1.74 1.76 1.77])
med =
    1.7690
des =
    0.0713