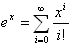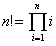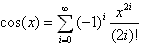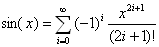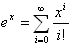Laboratorio 8 - Algoritmos iterativos - for, while, do-while
| Asignatura: Fundamentos de Informática |
 |
 |
| Especialidad: Electrónica - UPV/EHU |
| Curso académico: 2009-2010 |
| Profesor: Ismael Etxeberria Agiriano |
Entregables
Al finalizar la práctica será preciso guardar los
programas fuente:
08-003.c,
08-004.c,
08-005.c,
08-006.c,
08-007.c,
08-008.c,
08-009.c y
08-010.c.
Ejercicios - Programación en C
- 08-001: (Resuelto: 10 min)
Análisis.
Diseña el diagrama de flujo y codifica un programa que
lea un número positivo o nulo n
y escriba la palabra "Hola" n veces.
Si el número no es positivo o nulo
escribirá un mensaje de error y finalizará.
Al finalizar preguntará si se quiere volver a repetir
la operación.
En caso afirmativo se volverá al comienzo.
Diagrama de flujo con while.
Codificación laboratorio con while.
Diagrama de flujo 07-001 con for.
Codificación laboratorio 07-001 con for.
Diagrama de flujo con for.
Codificación laboratorio con for.
- 08-002: (Resuelto: 15 min)
Análisis.
Diseña y codifica un programa que
lea un número n mayor que 1 y diga si
n es primo.
Si el número no es válido escribirá un mensaje de error.
Al finalizar preguntará si se quiere volver a repetir
la operación.
Diagrama de flujo con while y variable booleana.
Codificación laboratorio con while y variable booleana.
Diagrama de flujo con for y break.
Codificación laboratorio con for y break.
Diagrama de flujo variante con for y break.
Codificación laboratorio variante con for y break.
Codificación laboratorio variante con while.
Codificación laboratorio variante con for sin break.
- 08-003: (10 min) Análisis.
Diseña y codifica un programa que
lea un número positivo n y muestre en pantalla todos
sus divisores.
Si n no es positivo se mostrará un error.
Al finalizar el cálculo nos preguntará si queremos volver a realizar la
misma operación con otro número.
- 08-004: (15 min) Análisis.
Diseña y codifica un programa que
lea dos número positivos n y m y obtenga el máximo común
divisor entre ellos.
El máximo común divisor de dos números es el mayor de sus divisores comunes.
Si m o n no son positivos se mostrará un error.
Al finalizar el cálculo nos preguntará si queremos volver a realizar la
misma operación con otros números.
Ejemplos (a comprobar):
- Máximo comun divisor (5, 3): 1
- Máximo comun divisor (6, 9): 3
- Máximo comun divisor (8, 4): 4
- Máximo comun divisor (24, 36): 12
- 08-005: (15 min) Análisis.
Diseña y codifica un programa que
lea dos número positivos n y m y obtenga el mínimo común
múltiplo entre ellos.
El mínimo común múltiplo de dos números es el menor de sus múltiplos
comunes distinto de cero.
Si m o n no son positivos se mostrará un error.
Al finalizar el cálculo nos preguntará si queremos volver a realizar la
misma operación con otros números.
Ejemplos (a comprobar):
- Mínimo comun múltiplo (2, 4): 4
- Mínimo comun múltiplo (5, 3): 15
- Mínimo comun múltiplo (9, 6): 18
- Mínimo comun múltiplo (3, 10): 30
- Mínimo comun múltiplo (12, 18): 36
- 08-006: (10 min) Análisis.
Diseña y codifica un programa que
lea un número positivo n y lo escriba con un separador de
puntos para los millares.
Utiliza enteros largos para poder comprobar el funcionamiento con números
mayores.
Ejemplos (a comprobar):
- 100: 100
- 1238: 1.238
- 100000: 100.000
- 1000000: 1.000.000
- 08-007: (5 min) Análisis.
Diseña y codifica un programa que
lea un número natural n y calcule el factorial de n
(n!).
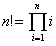
- 08-008: (15 min) Análisis.
Diseña y codifica un programa que
lea un ángulo en radianes x y calcule su coseno,
utilizando el desarrollo de Taylor con un error
(valor absoluto de la diferencia entre dos aproximaciones)
inferior a 0,000001.
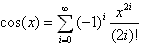
- 08-009: (10 min) Análisis.
Diseña y codifica un programa que
lea un ángulo en grados g, lo pase a radianes x
y calcule su seno,
utilizando el desarrollo de Taylor con un error
(valor absoluto de la diferencia entre dos aproximaciones)
inferior a 0,000001.
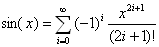
- 08-010: (10 min) Análisis.
Diseña y codifica un programa que
lea un número x y calcule ex,
utilizando el desarrollo de Taylor con un error
(valor absoluto de la diferencia entre dos aproximaciones)
inferior a 0,000001.