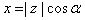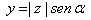| Asignatura: Fundamentos de Informática | |
|
| Especialidad: Electrónica - UPV/EHU | ||
| Curso académico: 2013-2014 | ||
| Profesor: Ismael Etxeberria Agiriano |
Este laboratorio trata de números complejos y para ello vamos a hacer un escueto repaso. Se supone que el alumno domina la matemática subyacente por lo que no se pretende proporcionar un monográfico detallado.
Podemos representar un número complejo z
de forma binómica
mediante su parte real x
y su parte imaginaria y multiplicada por i, que equivale
a 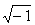 :
:
z = x + iy
Un número complejo puede considerarse un vector en R2
representable en el plano cuyo módulo es:
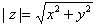
El conjugado de un número complejo es su simétrico respecto del eje
real.
Dado un número complejo en forma binómica z = x + iy
su conjugado 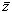 es:
es:
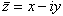
El opuesto de un número complejo z
es su simétrico respecto del origen:
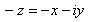
Para sumar dos números complejos en forma binómica se
suman las partes reales y las partes imaginarias:
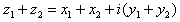
Restar dos números complejos será equivalente a sumar al primero
el opuesto del segundo.
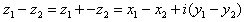
Para multiplicar dos números complejos en forma binómica
se procederá a multiplicar los términos, sabiendo que i*i es -1:
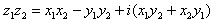
Podemos representar un número complejo z
en forma polar
mediante su módulo r
y su argumento α:
z = (r, α)
Si bien un mismo número complejo puede expresarse mediante infinitos
argumentos habitualmente utilizaremos el argumento principal,
que es el que se encuentra en el intervalo (-π, π).
Para multiplicar dos números complejos en forma polar bastará con multiplicar
sus módulos y sumar sus argumentos, es decir:
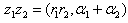
Para dividir dos números complejos en forma polar
bastará con dividir
sus módulos y restar sus argumentos, es decir:
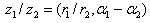
Ya hemos visto cómo obtener el módulo:
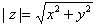
El argumento se puede obtener:
α = argctg(y/x)
Para convertir de forma polar a forma binómica tendremos que calcular la
x y la y.