| Asignatura: Fundamentos de Informática | |
|
| Especialidad: Electrónica - UPV/EHU | ||
| Curso académico: 2013-2014 | ||
| Profesor: Ismael Etxeberria Agiriano |
for, uno dentro del otro, con
i y j de contadores.
En nuestro caso haremos algo similar con dos bucles while.
f se inicializa
al elemento neutro de la suma, el 0.
f al
cálculo de i+2*j
(con los valores actuales de i y j).
n ó m
fueran inferiores al valor inicial (0 y 1 respectivamente)
el resultado dará 0 ya que no se terminan
de ejecutar ninguna vez ambos sumatorios.
r se inicializa al dividendo (37) y
mientras éste sea
superior al divisor (11) se irá restando al resto el divisor:
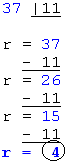
|
c:
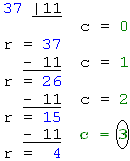
|
p, la primera potencia de 2 superior
al número,
y mirar sucesivamente para todas las potencias inferiores
si el dígito es 1 ó 0 (por tratarse de base 2).
p la primera potencia
de 2 superior a 37, a saber, 64.
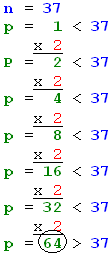
|
p por 2, como se ve en la Figura 7i.4.
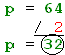
|
n/p es 1 ó 0,
que será el dígito para esa posición.
De hecho podemos escribirlo.
p a n.
p por 2.
como se ilustra en la Figura 7i.5.
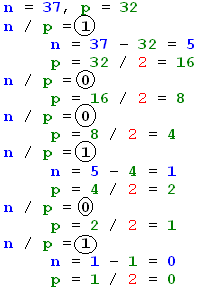
|
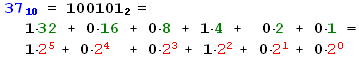
|
for pero vamos a hacerlo con una estructura
while.
x y un contador a 0
y vamos incrementando el resultado y el contador mientras
éste sea inferior a y.
i = 1 hasta y de
x y lo natural es resolverlo mediante un bucle
for pero en este laboratorio lo haremos con un
while.
for
para escribir n líneas, pero construida mediante
una estructura while.
i-ésima
(cuántos espacios y cuántos asteriscos).